Если матрица 
— квадратная, то обратной к ней матрицей называется такая матрица 
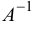, для которой справедливо двойное равенство
где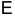 
— единичная матрица.
Квадратная матрица имеет обратную лишь в том случае, если её определитель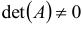 
. В этом случае она называется неособенной, или невырожденной. Например, для матрицы её определитель 
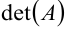не равен нулю:
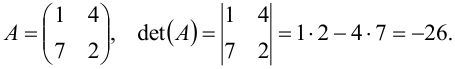
Матрица неособенная. Всякая неособенная (невырожденная) матрица имеет обратную матрицу.
Обратная матрица квадратной матрицы вычисляется по формуле
где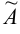 
— называется присоединенной матрицей. Присоединенная матрица — это матрица алгебраических дополнений элементов транспонированной матрицы .
Формула (1.8) для матриц второго и третьего порядков имеет вид:
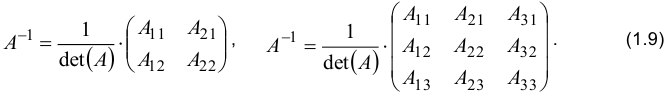
Пример:
Определить обратную матрицу (если она существует) для матриц: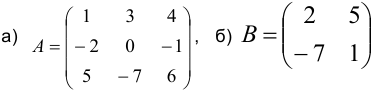 
.
Решение:
а) Определитель матрицы , 
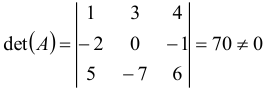, следовательно матрица невырожденная. Обратная матрица 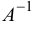для матрицы существует. Находим алгебраические дополнения элементов матрицы . Для этого определяем миноры элементов и присваиваем им знак согласно формуле (1.5):
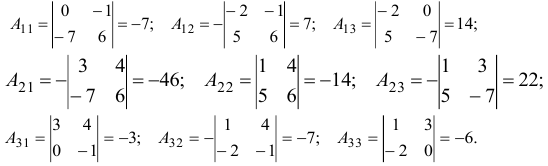
По формуле (1.9) запишем обратную матрицу:
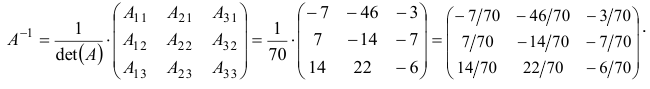
б) Определитель матрицы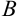 
, 
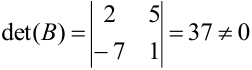, матрица невырожденная. Миноры элементов определителя второго порядка определители первого порядка. Определитель первого порядка содержит только один элемент и равен этому элементу. Находим алгебраические дополнения элементов матрицы 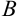. Для этого определяем миноры элементов и присваиваем им знак согласно формуле (1.5):
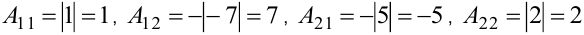. Тогда
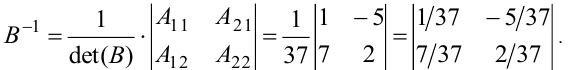
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
