Обратная матрица с решением задачи

Обратная матрица

Матрица называется невырожденной, если ее определитель отличен от нуля.

Матрица 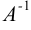называется обратной квадратной матрице , если .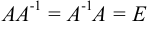

Теорема. Для того, чтобы матрица, обратная матрице , существовала, необходимо и достаточно, чтобы матрица была невырожденной.

Теорема. Для невырожденной матрицы существует единственная обратная матрица.

Матрицу, обратную матрицей 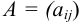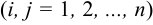, можно найти по формуле

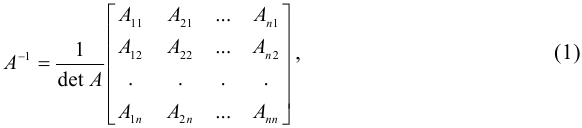
где 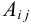— алгебраическое дополнение элемента 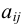матрицы .

Задача №5.

Выяснить, существует ли матрица, обратная матрице

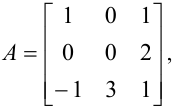
и если существует, то найти ее.

Решение:

Так как 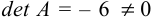, то матрица невыраженная и 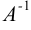существует.

Найдем 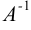по формуле (1). Алгебраические дополнения элементов матрицы :

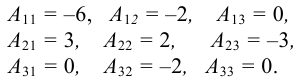
Следовательно,

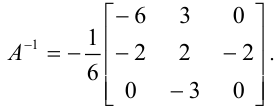
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:

Решение задач по высшей математике

Возможно эти страницы вам будут полезны:

Операции над матрицами задачи с решением

Определители задачи с решением

Ранг матрицы задачи с решением

Матричное решение системы линейных уравнений задачи с решением