Обратная матрица

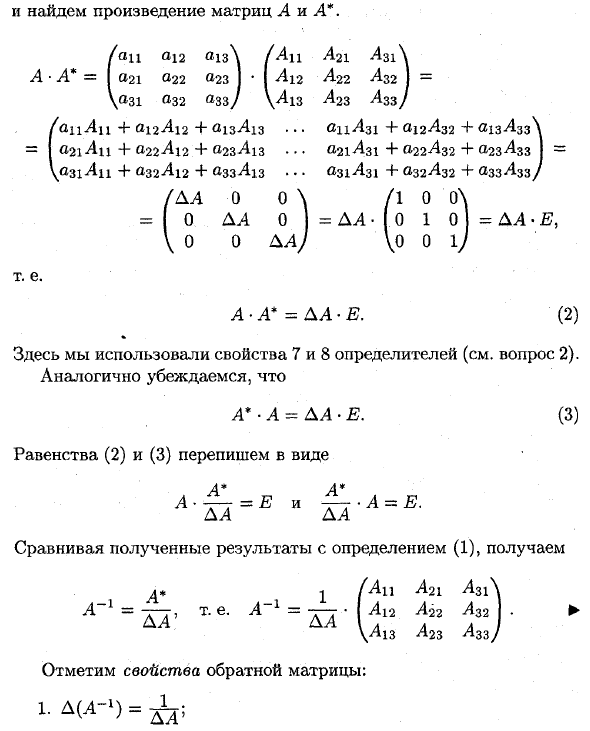
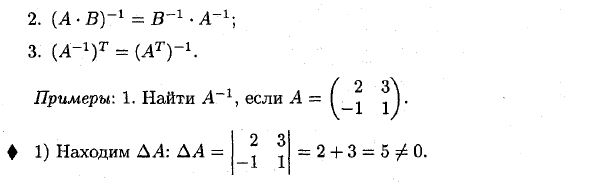
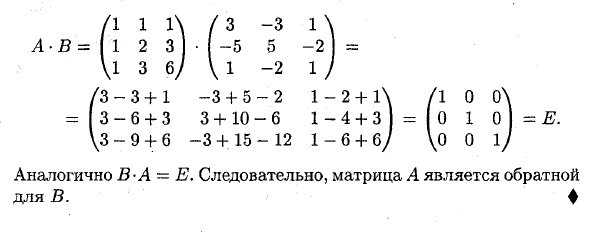
Обратная матрица

• Обратная матрица Пусть A — квадратная матрица n-го порядка Fan ai2 •• ain \ A = 0,21 «22 •• 0,2 р \ Gnl Op2 • Opp / Если определитель A A не равен нулю, квадратная матрица A называется невырожденной: A AÀ0. В противном случае (A A = 0) матрица A называется вырожденной. Матрица, сопряженная с матрицей A, называется матрицей (A21 .. ^ PL A * = A \ 2 A22. • Ap 2 A2p. APP / Где Aij — алгебраическое дополнение элемента a ^ данной матрицы A (определенное так же, как алгебраическое дополнение определителя). Матрица A ~ 1 называется обратной матрицей A. A • A ~ l = A ~ l-A = E, (1) Где E — единичная матрица того же порядка, что и матрица A. Матрица A ~ 1 имеет те же размеры, что и матрица A.

Теорема 1. .Выполните доказательство для кубической матрицы. Дай мне («Ai2 # 13 a2i a-22 «23 |> A A ^ 0. 「31」 32 「33 Настройте матрицу объединения / Ap An Az \ A * = J Au A-22 A32 \ Ai3 L03 ^ 33

Каждая невырожденная матрица имеет обратную матрицу Людмила Фирмаль

Найдите произведение матриц A и A *. («11» 12 «13 21 '' 22 23 » 31 « 32 » 33, Тан Ли + «12 ^ 12 +» 13 ^ -13 «21 ^ q +» 22 ^ 12 + «23 ^ 13» 31 ^ 11 + «32 ^ 12 +» 33 ^ 13 AC A2I скумбрия A22 L32 I = AlZ ^ 23 LZZ, , , , «CLxx +» 12 ^ 32 + «13 ^ 33 \ ••• «21 ^ 31 4-a22Az2 +» 23 ^ 33) = … «31 ^ 31» 32 ^ 32 + «33 L33 / / A A • 0 0> \ / 1 0 = 0 AL 0 = AL- 0 1 0 = AL \ o 0 AL, / V0 0 J A- A ‘= AL • E. 1 (2)% Мы использовали определяющие свойства 7 и 8 (см. Вопрос 2). Точно так же, (3) A * • A-AL • E.

Перепишите уравнения (2) и (3) в виде A *> A • — = E и • А = £. AL AL Результаты, полученные в определении (1), сравниваются следующим образом: Это 4 * 1 4 «1 — L из них» 1 — АAL ‘T’ ~ AL (A21 AzL Ах ах а32. A23 Ag) Обратите внимание на свойство обратной матрицы. 1. Ал 1. A (L-1) = i—

• (A-B) ~ l = B ~ l • L-1; 3. (Λ1) r = (Λ *) — 1. Пример: 1. Для A найдите A. 2 3 ♦ 1) Поиск ДА: ДА =. = 2 3 «-1 1 2 + 3 = 5 ^ 0. 2) Найти A *: An = 1, A2 \ = -3, Ax2 = — (- 1) = 1, A22 = 2, следовательно, A * = ^ j 2) • -1. l-1-1’1 «3 3) Найти A-1: L-1 = ^ 1 2) = ^ Проверить: 2,3 _ б, б 5,5,5 г _1 4- 1 3, 5 5 5 5 ♦ 2. Определите, какое значение А имеет обратную матрицу. A = Все невырожденные матрицы имеют обратную матрицу. Найти определитель матрицы А. Да = 1-2 2 L 3 0 = 3-0 + 2A-12-9 + 2A = 4A-9,2 1 1 A = ♦ Найти произведение матриц A и B. Для 4A-9Φ0, или AΦ, DAΦ0, или матрица A, невырождена и наоборот. ♦ 3. Покажите, что матрица A противоположна B A «A-1 =

2) Найти A *: An = 1, A2 \ = -3, Ax2 = — (- 1) = 1, A22 = 2, следовательно, A * = ^ j 2) • -1. l-1-1’1 «3 3) Найти A-1: L-1 = ^ 1 2) = ^ Проверить: 2,3 _ б, б 5,5,5 г _1 4- 1 3, 5 5 5 5 ♦ 2. Определите, какое значение А имеет обратную матрицу. A = Все невырожденные матрицы имеют обратную матрицу. Найти определитель матрицы А. Да = 1-2 2 L 3 0 = 3-0 + 2A-12-9 + 2A = 4A-9,2 1 1 A = ♦ Найти произведение матриц A и B. Для 4A-9Φ0, или AΦ, DAΦ0, или матрица A, невырождена и наоборот. ♦ 3.

Покажите, что матрица A противоположна B A «A-1 = Людмила Фирмаль

Смотрите также:

Предмет высшая математика

Матрицы (основные понятия)	Ранг матрицы
Действия над матрицами	Системы линейных уравнений (основные понятия)