Обратимые процессы

Обратимые процессы

• Обратимый процесс Некоторое равновесное состояние(7 \ V,…Из другого равновесного состояния(T \ V’,…Изменение термодинамического состояния системы при переходе к (а). в частности, речь пойдет о циклах, когда начальным и конечным состояниями являются same. It казалось бы, желательно определить путь, по которому будет происходить какой-то процесс, и задать

промежуточное состояние. Однако это нельзя сделать напрямую, так как параметры состояния системы, такие как температура, строго определяются только как характеристики системы в равновесном состоянии. Тем не менее, при таком рассмотрении этой трудности можно избежать, создав общую классификацию процессов. В термодинамике процессы делятся на 2 категории: обратимые

и irreversible. An примером необратимого процесса является выравнивание перепадов температуры, давления, концентрации и др., то есть переход в термодинамическое равновесное состояние. Если необратимые процессы протекают очень интенсивно, например, газ

Такие процессы не могут осуществляться в обратном направлении, не вызывая изменений в состоянии окружающего организма. Людмила Фирмаль

устремляется в вакуум, то происходит макроскопическое движение. Кинетическая энергия такого движения под действием сил трения превращается в тепло, а турбулентный поток, создаваемый в Газе в промежуточном состоянии, затухает, и в конечном итоге его заменяет равновесное состояние. Только после этого Состояние системы снова определяется термодинамическими переменными. Можно представить себе ограничительный случай процесса, который может полностью сохранить значение параметров состояния

системы. Это процесс, который выполняется таким образом, что каждое промежуточное состояние практически не отклоняется от равновесного состояния до Infinity. As как правило, вы можете подойти к этому делу и выполнить процесс очень медленно или разбить его на очень маленькие части stages. At предел, это обратимый процесс, так как он может осуществляться в обратном направлении на каждом этапе и осуществлять бесконечно малые

изменения внешних условий, не вызывая других воздействий. Понятие обратимого процесса идеализировано, но»спонтанный»процесс, который мы наблюдаем в макроскопическом масштабе, протекает только в одном направлении, то есть в направлении равновесия, как мы видим, очень важно для понимания термодинамики. Заметим, однако, что отправной точкой этого равномерного движения является механическое движение. Движение полностью определенной динамической системы может быть обращено вспять, не вызывая никакого другого эффекта, если все направления скорости reversed.

• It предполагается, что отсутствует сила трения. С этой оговоркой механическое движение можно рассматривать как прототип обратимых процессов. Обратимость таких движений обусловлена тем, что уравнение механического движения является квадратичным уравнением относительно времени. Действительно, обратимость механического движения не полностью совпадает с предельным случаем, рассматриваемым в термодинамике, оно очень медленно

или малыми шагами обрабатывает непрерывное состояние, бесконечно близкое к равновесию. Некоторые авторы, имея в виду это различие, называют соответствующий термодинамический процесс квазистатическим и сохраняют чисто механическое значение термина «обратимый».Эти характеристики. Термодинамическое и механическое описание отсутствуетЕсли принять во внимание противоречие, то ситуация уже отмеченная, то термодинамическое описание очень малого состояния определяет величину

механической variable. In 1932, Нильс Бор выразил это в своей лекции о памяти Фарадея： Например, термодинамическая необратимость, которая выражается в выравнивании температуры, не означает, что невозможно повернуть ход событий вспять, но показывает, что невозможно сделать описание такого обратного процесса, используя только понятие температуры различных тел. Потери энергии в необратимых процессах. Рассмотрим работу, которую выполняет

Для простоты будем считать, что система представляет собой идеальный газ 1 моль, расположенный в цилиндре, закрытом поршнем Людмила Фирмаль

организм, преодолевая действие внешних сил, и тем самым С. С. Г-1.—、 Шшшш： P = RT / V от t.. 1. Его поверхность смещается. (Рис.4).Во-первых, предположим, что роль внешних сил играет постоянное давление еше, которое представляет собой сумму атмосферного давления и веса поршня на единицу поверхности, а вся система

погружена в термостат, который поддерживает температуру системы постоянной до Т. С момента поршня начинает работать система охлаждения. consider. At равновесное давление газа поршня P = RTjV фиксируется в положении, соответствующем объему V в. при отпускании поршня он начинает двигаться вверх и останавливается в положении, соответствующем объему V ^(возможно, после определенного числа колебаний). Давление Pf балансирует точно

с внешним давлением Pb, 1esh. Однако первоначально кинетическая энергия передается в piston. In кроме того, в Газе происходит макроскопическое движение. Эти сложные промежуточные состояния исчезают под действием различных сил трения, в результате чего кинетическая энергия преобразуется в heat. So, независимо от предыдущего состояния газа, немедленно

устанавливается новое равновесное состояние(VT). Единственной особенностью процесса, важной с точки зрения термодинамики, является то, что была проведена определенная работа. ^ необр = Лшеш(Ы Ф-Ви) — (1.25） Эта работа, по-видимому, не равна всей энергии, высвобождаемой при расширении, поскольку часть энергии уходила на преодоление силы трения, как это всегда бывает при

необратимом processes. In в этом эксперименте система выполняет работу, которая определяется соотношением (1.25). Как увеличить эту работу? Очевидно, для этого необходимо оказывать внешнее давление на СЗ. Но мы В этом случае поршень движется в противоположном направлении, поэтому он не может быть выше равновесного давления газа I. В зависимости от расположения поршня, например, с помощью устройства из пружин и блоков, когда

внешнее давление поддерживается равным Явнеш = Р (1л Т), достигается оптимальный вариант. И, конечно же, движение будет бесконечным slow. It достигает ограничительного случая, который соответствует обратимому процессу. Работа в этом случае будет равной Up = J Pvnesh (Y)dV = ya J — = RT в ZL. (1.26） Это наибольшая ценность работы за счет изотермического расширения газов. Необратимо process. It может выполняться по-разному, между

фиксированными значениями. Объем Vi и Vf>в любом случае ^ необр <^ Арр-о-27） 13 окончательный выбор= PRI Это не сделало бы никакой работы вообще: Lneobr =0.Такие случаи происходят в эксперименте Гей-Люссака, упомянутом в§ 3, пункт 2. Необратимые стадии в любом процессе всегда приводят к диссипации механической энергии. Эффективность процесса снижается за счет трения, под его воздействием кинетическая энергия связана с макроскопическими движениями, вихрями и др. преобразуется

в тепло. Этот переход от упорядоченного макроскопического движения к хаотическому молекулярному движению обычно называют диссипацией энергии. Все макроскопические процессы более или менее необратимы, но зачастую сам процесс оказывается ближе к обратимым, чем человек предполагает. Приведенные выше примеры изучаются в detail. As оказалось, давление достигает

равновесного значения очень быстро, поэтому при рассмотрении поведения давления все процессы, протекающие со скоростью вплоть до скорости звука, можно считать бесконечно медленными. С другой стороны, из-за относительно медленного теплообмена, требуется гораздо больше времени, чтобы установить равновесную температуру. Хорошо известным примером является быстрое сжатие

и расширение воздуха в звуковых волнах. Эти процессы настолько медленны, что распадаются очень слабо под действием трения, поэтому их можно с большой точностью считать обратимыми. Однако она Адиабатична (не изотермична), потому что температура не может следовать за таким резким изменением давления. 2.Обратимое изменение идеального газа. Мы уже

рассматривали обратимый процесс изотермического расширения газов. Например, если вы используете уравнения фактического состояния газа, описанные в форме (1.7), вы не ограничиваетесь рассмотрением идеальных газов. Однако, рассмотрение идеального газа В данном конкретном случае работа выполняется из-за тепла, поступающего из высокотемпературного резервуара, а температура газа остается постоянной, что очень beneficial. It получается из общего

уравнения закона 1-го закона термодинамики Q = kU L. где член&U изотермического процесса равен нулю. Если внутренняя энергия идеального газа, идеального газа、 Функция температуры t только. Читатели могут заметить, что этот процесс можно использовать и в соответствии с формулой (1.26), как правило, для получения неограниченного количества энергии из резервуара. Однако это не может быть использовано в тепловом двигателе. Это связано с тем,

что приходится произвольно допускать значительное увеличение объема, что, естественно, делает невозможным проведение кругового процесса. Теперь рассмотрим процесс теплоизоляции Q = — O, когда газ расширяется под теплоизоляцией. Температура газа в этом случае снижается, поскольку работа выполняется за счет внутренней энергии. L = — Q = 0 или позже (1.28） Для того чтобы процесс был обратимым, внешнее давление поршня, как и прежде, не должно

сильно отличаться от равновесного давления, которое определяется уравнением состояния/(H, 7 \ V)= 0.Но температуры т уже нет constant. It определяется другими переменными из условия, что процесс должен быть адиабатическим. йй = 0 = {У.) ТДВ + [* л.) ВДТ + ПДВ. (1.29） Для идеального газа (d (J / dV) r = 0 и (dU \ dT) v = Cv% 、 0 = CvdTJrPdV. (1.30） Кроме того, для идеального газа P = RTjV разделение

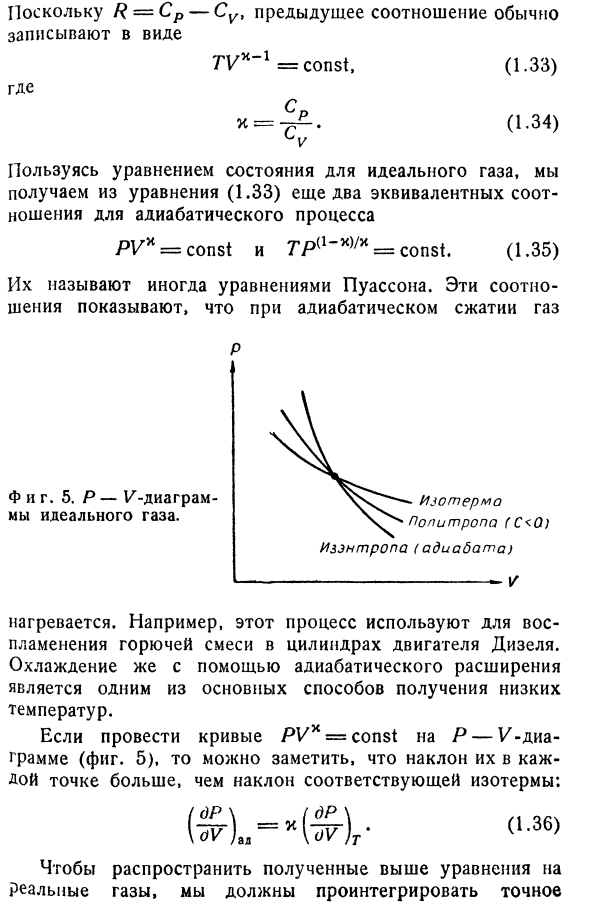
переменных будет、 =(1.31） (1.32） Или ТВК / ЧВ _ константный>С тех пор как/? = CP-Su, предыдущее соотношение обычно TV * ’1 = const, (1.33） Куда? С тех пор к = Соотечественник попиропа(с <0） Изотопы(Эдиа летучая мышь） И фигура тоже. 5. P-V диаграмма идеального газа. Он нагревается. Например, этот процесс используется для воспламенения горючей смеси в цилиндрах

дизельного двигателя.1. охлаждение путем адиабатического расширения является одним из основных способов получения низких температур. Если мы нарисуем кривую УХХ = const на диаграмме P — — — (рис. 5), мы увидим, что наклон в каждой точке больше, чем наклон соответствующей изотермы. Чтобы распространить полученное выше уравнение на реальный газ, точное (1.34） Используя уравнение состояния идеального газа, можно получить еще 2 эквивалентных

соотношения процесса теплоизоляции из уравнения (1.33). PV * = const и = const (1.35） Иногда называют уравнением Пуассона. Эти соотношения обусловлены тем, что газ при адиабатическом сжатии Коэффициент, который объясняет процесс теплоизоляции： О = CvdT + [[%л)т + п \ дв,(1.37） Зачем нужно знать уравнение состояния газа. Например, можно использовать уравнение ван-дер-Ваальса, как это сделано в задаче Sec. Если требуется 2,§ 7, пункт 1 или более высокая

точность, то по формуле (1.7). Конечно, изотермические и теплоизоляционные процессы-не единственно возможный процесс. Они представляют собой идеальный тепловой контакт между системой и термостатом и крайний случай полной теплоизоляции системы. Если вместо CpjCv взять показатель степени уравнения Пуассона в виде произвольного положительного значения,

то получим тип процесса, называемый политропой (см. Рис.5). в этих процессах система обменивается теплом с окружающим телом. dQ = CvdT + PdV f 0(1.38） Вычислите dQ политропного процесса. По формуле(1.33)、 дв = Т ^-^ ДТТ(1.39） Следовательно、 1 PV P ПДВ == Т ^^ взв = й; ДТ Ц1-40） йд = [ЧВ-^-т) ДТ. (1.41） Это означает, что количество тепла, подаваемого в систему при повышении

температуры на 1°, является постоянным*).Эта константа с = СV—(1.42） В зависимости от политропного показателя х может иметь различные значения. k = C равно нулю только для конкретного значения pjCv. Политронный процесс используется в технологии для представления различных энергетических циклов. Таким образом, политропный процесс можно определить как процесс, протекающий с определенной теплоемкостью. С= const.

Смотрите также:

Предмет термодинамика

Идеальный газ	Формулировки второго закона
Внутренняя энергия	Цикл Карно