Оглавление:

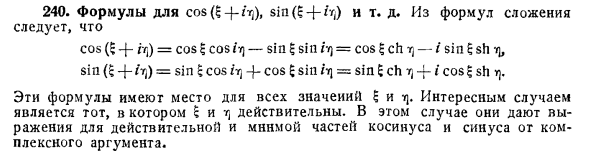
Обобщенные гиперболические функции
- Обобщенная гиперболическая функция. Пример LXXXVIII. 20 С chC и shC, определенные для фактического значения уравнения С ch; = j (expС-f exp (-С)), shС = (expС-exp (-С) . (I) Вы можете распространить это определение на сложные значения переменных. То есть мы можем согласиться с тем, что уравнение (1) считается определяющим ch C и sh C для всех действительных и комплексных значений C.
Читатели легко это подтверждают cos iС = chС, sin / С = / shС, ch / С = cosS, sh iС = * sinС. Людмила Фирмаль
| Общее значение а | Связь между логарифмической и обратными тригонометрическими функциями |
| Выражения синуса и косинуса через показательную функцию | Степенной ряд для ехрz |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Мы обнаружили, что основные тригонометрические выражения, такие как cos 2С = cos2С– sin2С, верны даже тогда, когда С допускает комплексные значения. Следовательно, когда cos C заменяется на cos / C, sin C заменяется на sin / C, а cos 2 C заменяется на cos 2 / C, то есть когда cos C заменяется на ch C, sin C на i sh £ и cos2C на ch2C поэтому ch 2t = chaC + sh4. Аналогичное преобразование применяется к тригонометрическим тождествам. Это объясняет соответствие, отмеченное в Примере LXXXVIII. Между 22 гиперболическими и нормальными тригонометрическими выражениями.
Формулы, такие как cos (E + rq) »sin (S + h). Из дополнительной формулы cos ($ — {- ir) = cos? потому что это] -sin £ sill h) = cos? ch tq- / sin 5 sh sin ($ — {- / r4) = sin $ cos ft) -f-cos £ sin it \ = sin £ ch tj -f-1 cos? ш т). Эти формулы применяются ко всем значениям и u. Интересный случай, когда S и r действительны.
В этом случае они дают косинус сложного аргумента и действительные и мнимые части синуса. Людмила Фирмаль

