Оглавление:


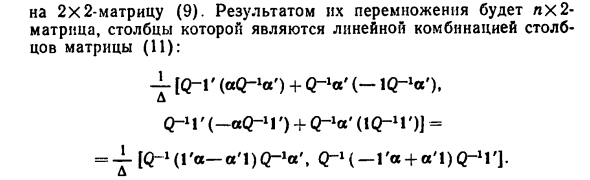
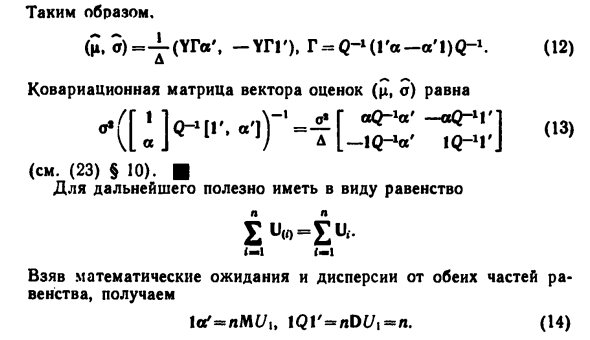

Обобщенная линейная модель для семейства сдвига-масштаба
- Рассмотрим независимую выборку Х \, Лг, …, Хп А) п. Ф ((х — ц) / о); ф. п. Ф (у) стандартизованных ел. в. с общей ф. С / (= (Х (Ю / о ,, = 1 п, В) считается известной, параметры и 0> н неизвестны. ) Орядковые статистики ел. В. А) и Б) связаны формулой ? / (/> — (* @ — | 0 / <». » -I п, C) и так как ф. п. С (у) ел. в. С /, известна, то в принципе любые <арактеристики? / <,> могут быть рассчитаны. o = a, -t cov (t / (o.U (j)) = qih i, j = l, …, n,
89 и, учитывая с), запишем X (i) = | x + at / (,) = n + aai + a (t / (.) — Он), i = l, …, n.D) Людмила Фирмаль
- Полагая ХA) = У,; t / (,) — a, = e ,, /=1,…,я, E) представим D) в виде обобщенной линейной модели: У, = ц + оа, + аег, i = \, …, n, F) или в векторной форме: Y = (ц, а) I I + oe, 1 = • A, …. 1), a— (av …. a ,,), Me —0, RB- 2. Наилучшие несмещенные оценки. Оценки ц, а вы по формелам B2) § 10: ! ^ [1 \ а ‘]) — (8) Производя перемножение, преобразуем последний сомножитель в (8) к 2х2-матрице и найденному матрицу: Г iQ-ir iQ-ia ‘1-1 = j r «Q-ia’ -aQ-Ц ‘1 LQЧ ‘Qi’J Д [IQ ^’ 1Q4 ‘J LaQ-Ч ‘aQ-ia’ где д = (IQ-Ч ‘) (aQ-‘o’) — AQVJ. A0)
Матрица, столбцы которой являются линейной комбинацией столбца столбцов матрицы A1): 4 «IQ-1 ‘(« О »’) + О * ‘(-lQ ^ o’), д Q-Ч ‘(—aQ-Ч’) + О »'(IQ-Ч’)] = !, Q-Ч— Га + а’1H-Ч ‘]. 90 Таким образом, (ц.а) = 4 — (* Га ‘, -YIV), Г = 0- »А’а-а’1Н ^. А2) Ковариационная матрица векторных оценок (ц, с) равна (см. B3) § 10). ¦ Для дальнейшего Взрыв математических ожиданий и дисперсий рав, получить 1ее ‘= лМ {/ ,, lQl’ = nD? /, = N.
Патричный множитель при векторе Y в формуле (8) произведению / гХ2-матрицы Q — ‘[l’. A ‘] = [Q-lV, Q-‘o’] A1) на 2х2-матрицу (9). Людмила Фирмаль
Смотрите также:
| Матрицы из случайных элементов | Симметричное распределение |
| Байесовский подход в статистике | Невырожденное нормальное распределение |
Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.

