Оглавление:
Обобщенные силы инерции
По той же методике (18.4), по которой вычислялись обобщенные силы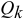 
, соответствующие активным задаваемым силам, определяются и обобщенные силы 
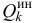, соответствующие силам инерции точек системы:
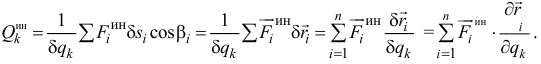
И так как
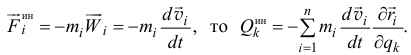
Немного математических преобразований.
Очевидно,
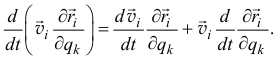
Отсюда
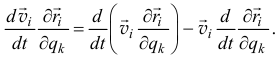
Так как
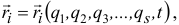
а
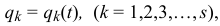
то
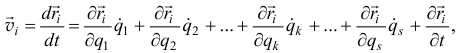
где
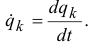
Значит, частная производная скорости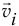 
по 
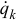
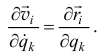
Кроме того, в последнем члене (18.9) можно поменять порядок дифференцирования
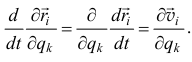
Подставляя (18.10) и (18.11) в (18.9), а потом (18.9) в (18.86), получим:
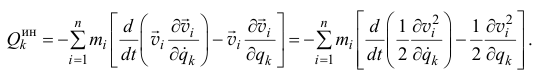
Разделив последнюю сумму на две и имея в виду, что сумма производных равна производной от суммы, получим:
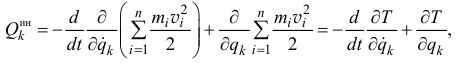
где
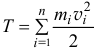
кинетическая энергия системы,
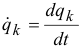
обобщенная скорость.
Уравнения Лагранжа
По определению (18.3) и (18.8а) обобщенные силы
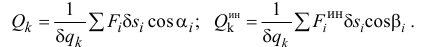
Сумма их
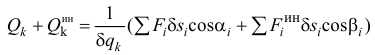
или
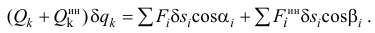
Но на основании общего уравнения динамики (17.3) правая часть равенства равна нулю. И так как все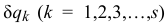 
отличны от нуля, то 
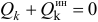. Подставив значение обобщенной силы инерции (18.12), получим уравнение:
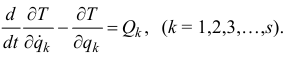
Эти уравнения называются дифференциальными уравнениями движения в обобщенных координатах, уравнениями Лагранжа второго рода или просто — уравнениями Лагранжа. Количество этих уравнений равно числу степеней свободы материальной системы.
Если система консервативная и движется под действием сил потенциального поля, когда обобщенные силы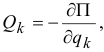 
уравнения Лагранжа можно составить по форме
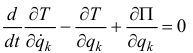
или
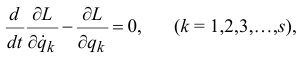
где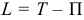 
называется функцией Лагранжа (предполагается, что потенциальная энергия 
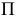не зависит от обобщенных скоростей).
Нередко при исследовании движения материальных систем оказывается, что некоторые обобщенные координаты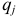 
не входят явно в функцию Лагранжа (или в 
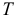и 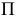). Такие координаты называют циклическими. Уравнения Лагранжа, соответствующие этим координатам, получаются проще. Так как 
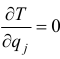и 
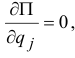то
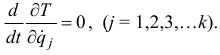
Первые интегралы последних уравнений находятся сразу. Они называются циклическими интегралами
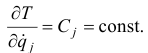
Дальнейшие исследования и преобразования уравнений Лагранжа составляют предмет специального раздела теоретической механики -«Аналитическая механика».
Уравнения Лагранжа обладают целым рядом достоинств в сравнении с другими способами исследования движения систем. Основные достоинства: методика составления уравнений одинакова во всех задачах, реакции идеальных связей не учитываются при решении задач.
И еще одно — эти уравнения можно использовать для исследования не только механических, но и других физических систем (электрических, электромагнитных, оптических и др.).
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Обобщенные силы |
| Уравнения равновесия Лагранжа |
| Теорема о движении центра масс |
| Теорема об изменении количества движения |
