Обобщенные координаты

Обобщенные координаты

Как уже говорилось, для определения положения механической системы, на которую наложено m двусторонних связей, достаточно задать только 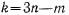каких-либо независимых параметров, полностью определяющих положение этой системы. Число независимых параметров равно числу степенен свободы системы. Каждая новая связь будет на единицу уменьшать число степеней свободы, а следовательно, и число независимых параметров, определяющих положение системы. Здесь всюду предполагается, что на систему наложены удерживающие связи. Независимые параметры, через которые могут быть выражены все декартовы координаты точек системы и которые полностью определяют положение последней, называются обобщенными координатами системы, или лагранжевыми координатами

(они были введены в механику Лагранжем). Эти лагранжевы координаты имеют вполне определенный геометрический смысл. Они вообще могут отличаться от декартовых координат, но могут также и включать в свое число одну или несколько декартовых координат. Обозначая k независимых параметров, через которые выражаются все декартовы координаты точек системы, через 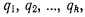будем иметь

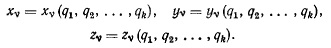
Во всех случаях, когда декартовы координаты различных точек системы могут быть выражены в явном виде через систему независимых параметров 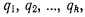(которые можно изменять независимо один от другого), полностью определяющих положение системы, будем называть такую систему голономнон, а сами параметры 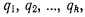-координатами голономной системы. В этом случае можно утверждать, что на систему наложено 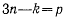различных связей. Если из k уравнений системы (а) определить величины 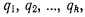в функции k величин из 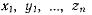и подставить в оставшиеся 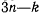уравнений (а), получим р зависимостей между координатами 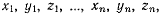которые и будут представлять собой уравнения связей. Условие разрешимости уравнений (а) относительно величин 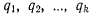сводится к тому, что в прямоугольной матрице из частных производных

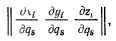
содержащей k столбцов и 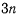строк, хотя бы один из миноров k-того порядка будет отличен от нуля, т. е. матрица имеет ранг k.

Пусть значения параметров 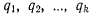определяют некоторое положение системы. Рассмотрим близкое к данному положение этой системы, которое определяется значениями параметров:

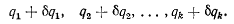
Тогда вариации декартовых координат получат вид

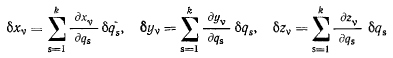
и все возможные перемещения системы можно будет задать при помощи вариаций независимых параметров 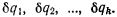Пусть на точку системы с координатами 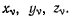действует активная сила 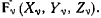Необходимое и достаточное условие равновесия

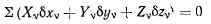
при помощи равенств (а) можно выразить через вариации независимых параметров

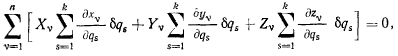
или, после изменения порядка суммирования,

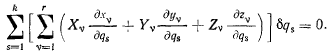
Обозначив через 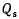выражение, стоящее в квадратных скобках

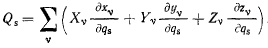
и перепишем уравнение (d) в виде

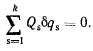
Величины 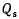называют обобщенными силами системы, соответствующими 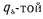обобщенной координате. В дальнейшем всегда будем предполагать, что параметры 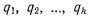выбраны так, что для каждого положения системы для любого 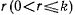существует перемещение, определяемое условиями

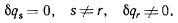
и нет перемещений, при которых все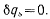

Так, например, положение точки, вынужденной оставаться на окружности 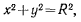определяется всего одним параметром. Но если в качестве такого параметра выбрать координату у, то при 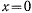частная производная 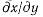теряет смысл и координата у перестает удовлетворять определению лагранжевых координат. Нетрудно видеть, что при 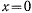возможному перемещению точки соответствует значение 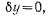а вариация координаты х становится неопределенной. Параметр у является координатой Лагранжа всюду, за исключением значений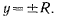

Так как все 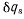совершенно произвольны и независимы, равенство (е) будет справедливо лишь тогда, когда все 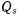обращаются в нуль, т. е. выполняются условия

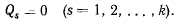
Полученные k уравнений равновесия называются уравнениями Лагранжа. Они определяют k неизвестных значений обобщенных координат 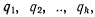соответствующих положению равновесия системы.

Выражение 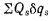представляет собой сумму работ всех активных сил, действующих на систему, на произвольном возможном перемещении системы, т. е.

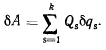
Если сообщить системе возможное перемещение, соответствующее изменению только одной обобщенной координаты, например перемещение, определяемое условиями

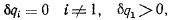
и подсчитать работу сил 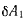на этом перемещении, то получим соотношение для определения обобщенной силы

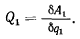
Так можно подсчитать все обобщенные силы системы.

Если существует силовая функция 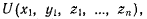то и, выразив силовую функцию через обобщенные координаты Лагранжа, получим

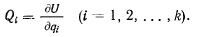
В качестве примера рассмотрим задачу о равновесии свободного твердого тела. Для определения его положения зададим координаты произвольной точки С твердого тела (рис. 130). Свяжем с точкой С декартову систему прямоугольных осей 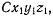перемещающихся поступательно, и систему 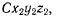неизменно связанную с твердым телом. Положение последней системы относительно осей 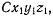определим углами Эйлера 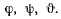Каждую из шести величин 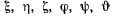можно изменять независимо от других. Все они полностью определяют положение твердого тела в пространстве. Если все названные параметры остаются неизменными, то не будет двигаться и твердое тело. Параметры 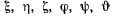являются определяющими координатами системы. Декартовы координаты произвольной точки твердого тела могут быть выражены через эти параметры. В самом деле, для произвольной точки твердого тела имеем

Записав таблицу направляющих косинусов углов, образованных осями 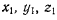с осями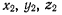

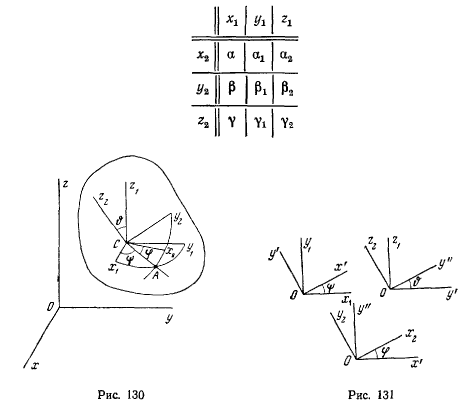
заметим, что система 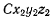может быть получена из системы 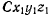тремя конечными поворотами (рис. 131), которые определяются следующими формулами преобразования:

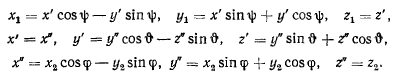
Тогда результирующее преобразование получит вид

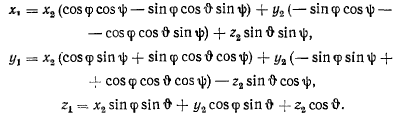
Сравнивая полученные формулы с выражениям»

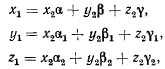
получим значения направляющих косинусов, выраженных через углы Эйлера

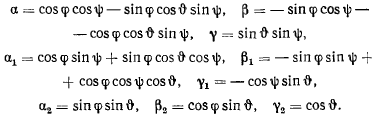
Эти формулы устанавливают явную зависимость декартовых координат от независимых параметров, определяющих положение твердого тела.

Возможные скорости точек 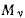твердого тела удовлетворяют формуле Эйлера

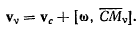
Для проекций возможных скоростей точек твердого тела на оси получим

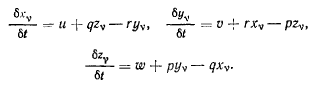
Отсюда сразу находим проекции возможных перемещений точек системы

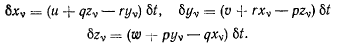
Полученные формулы устанавливают зависимость возможных перемещений от проекций мгновенной угловой скорости твердого тела 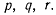Последние определяют только возможные перемещения твердого тела. Декартовы координаты x у, z точек твердого тела не могут быть выражены через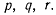

Предполагая, что на точки твердого тела действуют активные силы 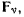запишем принцип Бернулли в виде

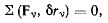
где

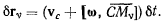
Тогда после подстановки будем иметь

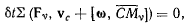
или

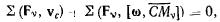
откуда следует

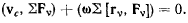
Это уравнение должно выполняться при любых возможных перемещениях твердого тела, находящегося в равновесии, т. е. при произвольных значениях 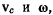что возможно, если удовлетворяются условия

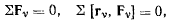
являющиеся известными уравнениями равновесия твердого тела.

Пример:

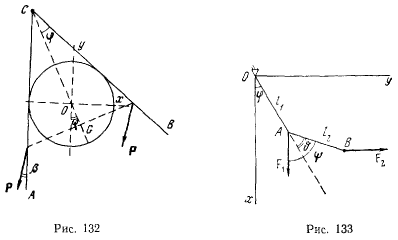
Два одинаковых стержня АС и СВ, каждый длиной 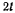и весом Р, связаны между собой шарниром С и опираются на неподвижный цилиндр радиуса r с горизонтальной осью (рис. 132). Найти угол 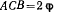при равновесии системы и угол который биссектриса этого угла составляет с вертикалью.

Решение:

Параметры 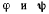полностью определяют положение системы и потому могут рассматриваться как лагранжевы координаты. Тогда уравнения равновесия получат вид

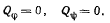
Первое из этих уравнении получаем, полагая что 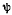не изменяется при возможных перемещениях системы. Определив координату 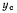центра тяжести системы

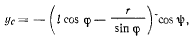
получим уравнение равновесия

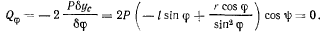
Полагая, что при возможных перемещениях но изменяется 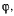получим

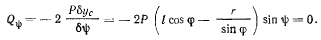
Этим уравнениям удовлетворяют следующие решения:

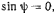что возможно только при 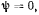и угол 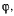определяется из уравнения

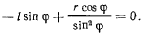
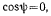что возможно, когда 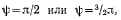угол 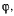здесь определяется из уравнения

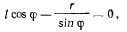
и, следовательно, должно бить выполнено условие 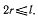Стержень АС не оторвется от цилиндра только тогда, когда угол 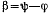будет отрицательным. Последнее выполняется только при 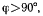что противоречит условию для определения .

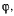Если 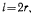то уравнения равновесия имеют еще одно решение: 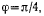образующее в нуль выражения, стоящие в круглых скобках.

Замечание. При определении обобщенных сил необходимо следить за тем, чтобы все обобщенные силы определялись в одной и той же системе независимых переменных. Поясним это на примере.

Пример:

Система состоит из двух материальных точек А и В, связанных между собой нерастяжимой нитью АВ длины и 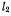соединенных с неподвижной точкой О нерастяжимой нитью длиной (рис. 133). К точке А приложена вертикальная сила 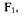к точке В — горизонтальная сила 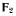Определить положение равновесия системы.

Решение:

Выберем сначала за независимые переменные углы 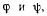которые образуют соответствующие нити с вертикалью. Определяй обобщенные силы в этой системе переменных, получим

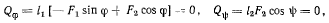
откуда имеем следующие условия равновесия:

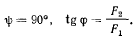
F-сли же за независимые переменные выбрать углы 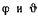( 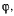определен выше, а 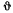угол между направлениями нитей), то уравнения равновесия получат вид

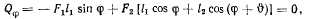
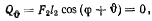
хотя условия равновесия и не изменяются.

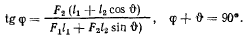
Пример:

Определить выражение обобщенной силы для твердого тела, способного вращаться вокруг неподвижной оси z.

Решение:

Возможное перемещение сводится к повороту вокруг не-подвижной оси. Примем эту ось за ось z. Тогда для определения проекций возможных перемещений можно будет записать матрицу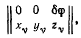

откуда будем иметь

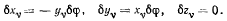
Подсчитывая работу активных сил на этом возможном перемещении,

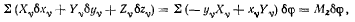
где

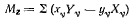
представляет собой сумму моментов активных сил относительно оси г, т. е. обобщенная сила сводится к моменту результирующей пары.

Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Принцип Торричелли

Связи и возможные перемещения

Общие теоремы о равновесии системы материальных точек

Метод неопределенных множителей Лагранжа