Оглавление:



Объемное напряженное состояние
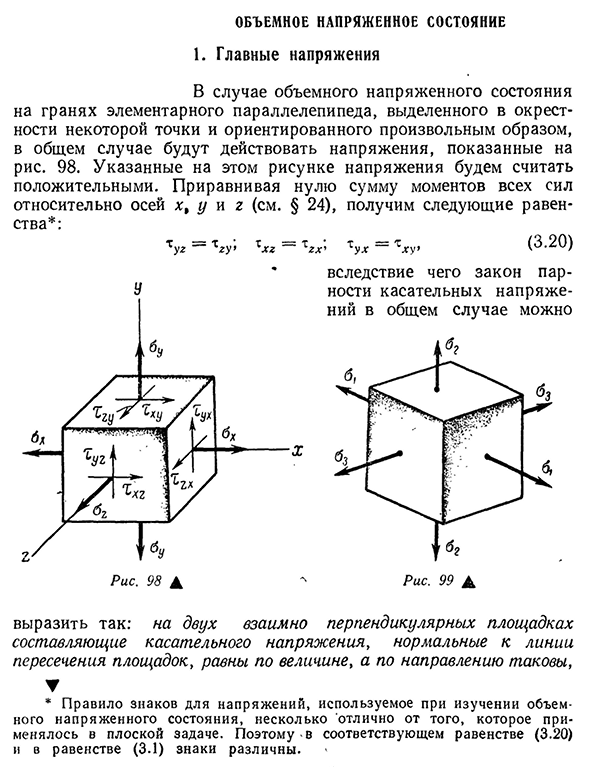
- Объемное напряженное состояние 1. Сетевое напряжение В случае объемного напряженного состояния на плоскости основного параллелепипеда, изолированного в окрестности точки и ориентированного каким-либо образом, как правило, напряжение показано на рисунке. 98 Напряжение, показанное на этом рисунке, считается положительным. Если мы суммируем моменты всех сил вокруг осей x, y и g (см. § 24) до нуля, мы получим следующее
уравнение *: буксир = TSU — гггх, ту = чт, (3.20) Рис 98А В результате закон тангенциального напряжения в общем случае имеет вид Рис 99А Для этого: для двух взаимно перпендикулярных компонентов платформы касательное напряжение, перпендикулярное линии пересечения платформ и равное по размеру, история *
Знаковые правила для напряжений, используемые в исследованиях напряженного состояния, немного отличаются от тех, которые Людмила Фирмаль
используются для плоских задач. Поэтому знак отличается для эквивалента (3.20) и эквивалента (3.1). 102 Люди, которые склонны поворачивать материальные частицы в противоположном направлении. Ранее мы видели, что любое плоское напряженное состояние возникает при двух взаимно перпендикулярных напряжениях (сжатии) основными напряжениями atah и amin. Аналогично, если состояние объемного напряжения меняет
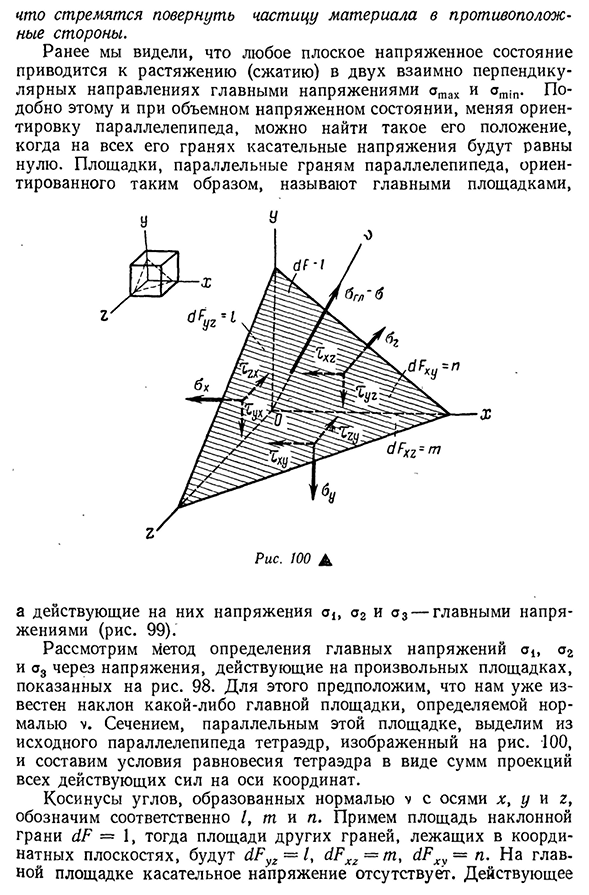
ориентацию параллелепипеда, вы можете найти положение, в котором все его касательные напряжения равны нулю. Сайт, параллельный плоскости параллелепипеда, ориентированного таким образом, называется основным сайтом, А напряжение А2 и А3, действующее на них, является основным напряжением (рис. 99). Рассмотрим, как определить основное напряжение A2 и A3. 98 через напряжение, действующее на любой участок, как показано на
- рисунке, для этого мы уже знаем наклон любого основного участка. Предполагая, что он определяется нормальным т. Сечением, параллельным этому участку, исходной прямой 100, и мы ставим условие тетраэдрического равновесия в виде суммы всех проекций действующей силы на оси координат. Принимая площадь наклонной плоскости dF = 1, площадь другой плоскости в координатной плоскости равна dFyz-l, dFxz = m, dFxy-p. активный 103 Desmain напряжение AGL указывает на a. Сумма предсказаний силы на оси x дает al-AH1-тое дерево n = 0. Проецирование всех сил на ось y и ось g дает два одинаковых уравнения. Таким образом, мы имеем
следующее уравнение триетраэдрического равновесия: (° x-a) 1 4- * x ut4-THG n = 0; ‘^ uh1 + (° y ~ °) t + V n =’ Xzxl + tgut4- (AG-a) N = 0. (А) Поскольку существует зависимость / 2 4-T2 4-P2 = 1, (b) между нормальными c-направляющими косинусами v, они не могут быть равны нулю одновременно. Из высшей алгебры известно, что при этом условии определитель системы (а) должен быть нулевым. (3,21) Раскрывая определитель (3.21), мы становимся кубическим уравнением o ^ — / ^ 4- / 2O_ / 3 = 0. (3.22) Три корня являются значениями трех основных напряжений alt A2 и O3
(основываясь на симметрии определителя D, они действительны для всех начальных напряжений AG, AU и т. Д.). Коэффициент уравнения (3.22) имеет Людмила Фирмаль
следующий вид: L ~ Ah + ° u4-I-a4-5 0 4-o a-T2 — T2-T2: / ‘8,. «О, да. RWY g-OHT2C g-OHT2X2-a g T2 4-2T t. X ты уй хз В частном случае условий плоского напряжения кубическое уравнение (3.22) представляет собой квадратное уравнение, дающее значения Ci и A2, два корня которых соответствуют ранее полученному уравнению (3.13), в данном случае исходной параллели Поверхность шестигранника HOU должна быть без напряжения, поэтому необходимо установить C, = 0, буксир = 0, HCH = 0. Чтобы найти t / n, соответствующее одному из трех основных напряжений A2 и A3, нам нужно подставить значение этого
основного напряжения в (a) вместо a. 104 Одно из трех основных напряжений является алгебраически максимальным в данной точке, самое низкое напряжение, обозначенное AI, равно 3, промежуточное -A2, т.е.> <* 2> a3- (3.23) Растягивающее напряжение все еще считается положительным и отрицательным при сжатии. Давайте посмотрим на основную закономерность распределения напряжений вдоль склона основного параллелепипеда (образованного основной платформой).
Смотрите также:
| Круг мора | Деформированное состояние в точке |
| Понятие о траекториях главных напряжений | Закон Гука при плоском и объемном напряженных состояниях |

