Объем тел вращения

Объем тел вращения

Объем тел вращения. Было отмечено, что в конце пункта 31.2 вводится понятие объема пространства, а также понятие площади на плоскости. Выведена формула для расчета объема вращающегося тела. Теорема 2.Продолжить функцию/(x) 0 на интервале [a, b] и O-объекты, полученные вращением изогнутой трапеции O, порожденной графом функции/.Далее, об объеме тезиса 2, Формула б Бумага С? = я $ / 2 (х) ух. (32.10)） Но… Доказательство. Он представлен хχ и стелой, образованной вращением ступенчатой формы ХХ и охох вокруг оси Ox (см. доказательства теоремы 1).Включение(32.3) из§ 32.Геометрическое и физическое применение интегралов 498. 7Т С. С =поэтому、 Тезис 7T ^тезис » 2 ^тезис C} x. (32.11).

И так как функция f является непрерывной и, следовательно, интегрируема. Людмила Фирмаль

• Объем множества dx-a 2T и сумма объемов цилиндра Vx, образованных вращением прямоугольника§xr и Cr | (рис. 125). К -Документы б 7м = 2 ЛТ? 1 = 1 К Yx =2 нм? Ах. I-1 И Y * низкий И верхняя сумма дарбу функций π/ 2(x).И так оно и есть.、 б ЧХ ^ п \ п(х) УГ ^ УГ、 (32.12） 、 Орел[Yx-Ut1 = 0.(32.13） Из неравенств (32.11) и (32.12)、 ВХ-ух ^ п \ р (х) ух-с C} » с V хНо… Таким образом, выражение(32.10) продолжается по формуле (32.13). В г = я | (Р2-Х2) ух-ng2x рН 3 ″ = 2lg3 -;; о lg3 = yag3 Образцы. 1.Найти объем V шара с радиусом R. рассмотрим этот шар как объект, образованный вращением полукруга r = y72-x2, и получим ось Ox (см. Рисунок 96)〜r ^ x ^ r в Формуле (32.10).

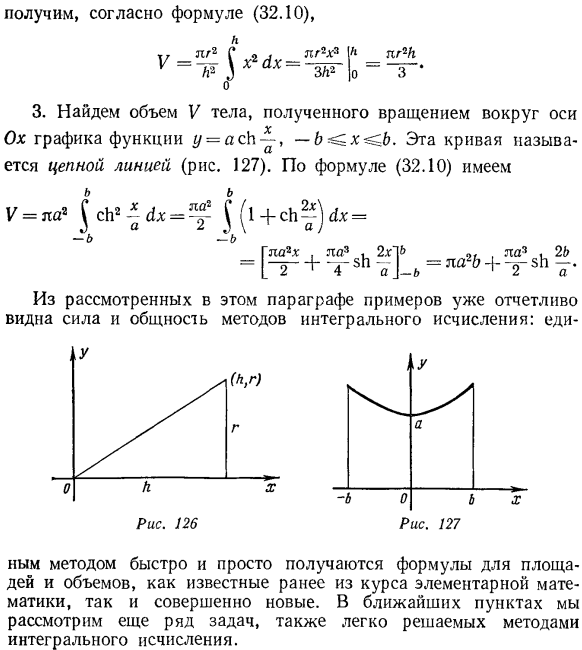
• Найти объем V прямой пирамиды высотой k и радиусом основания R. рассмотрим указанный конус как объект, полученный вращением треугольника с вершинами (0, 0), (k, 0) и (k, g) вокруг оси Ox (рис. 126）、 32.3.Вычисление длины кривой Четыреста девяносто девять По формуле(32.10)、 кг р. 3.Найти объем V объекта, полученный вращением графа функций y = acb -,-b ^ x ^ b вокруг оси Ox. Эта кривая называется цепной линией (рис. 127). по формуле (32.10)、 Г = по2 ^ СВ2 > с! Х = ^-^ 1 + уп ^ 2х = Б-б ’ Gyaa2x, Аа3, 2х \ Б 91, Аа3, 2б = [+Т 5б т. ТС = па Б + Т 5Б в.

Используя новый метод, вы быстро и легко получите как известные ранее формулы площади и объема, так и совершенно новые. Людмила Фирмаль

• Из примеров, рассмотренных в этом разделе, уже хорошо видны интенсивность и общность методов интегральных расчетов. Один. в ходе наивного mathematics. In в следующем параграфе мы рассмотрим множество задач, которые легко решаются методом интегрального расчета.

Смотрите также:

Предмет математический анализ

Свойства меры открытых множеств.	Вычисление длины кривой.
Вычисление площадей.	Площадь поверхности вращения.