Оглавление:


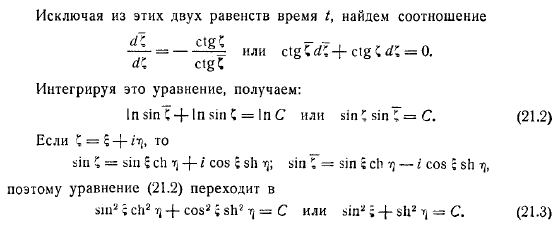

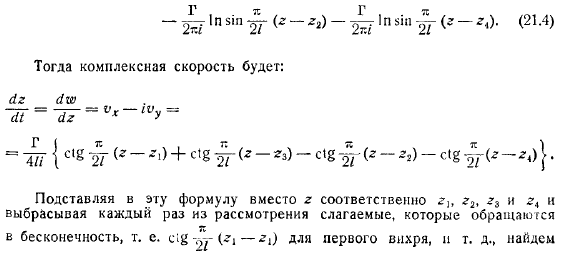

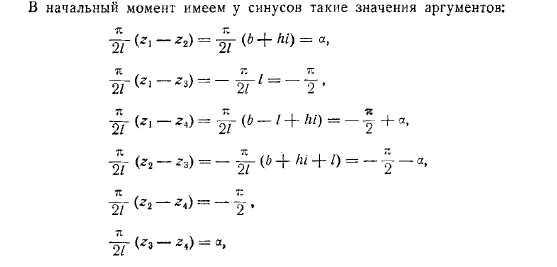

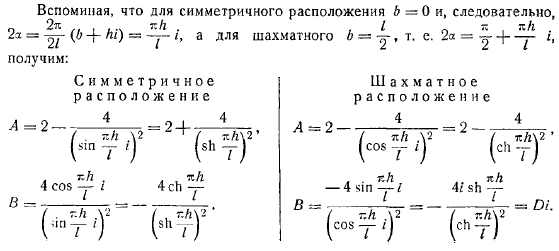





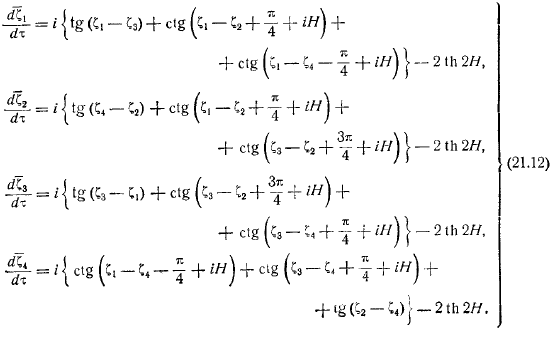

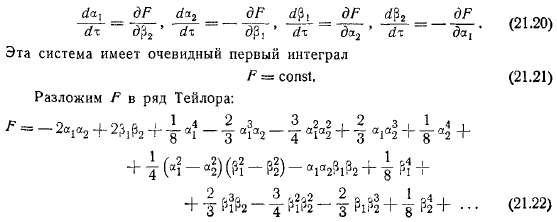


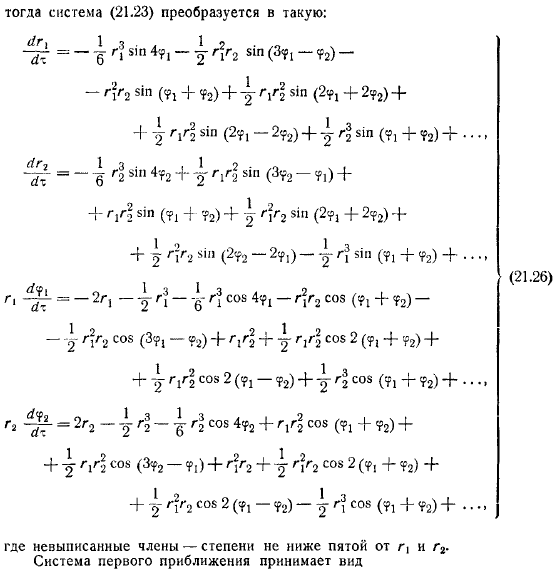
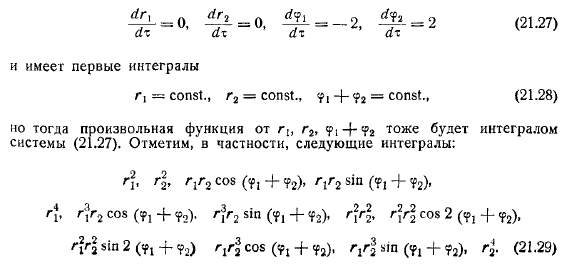

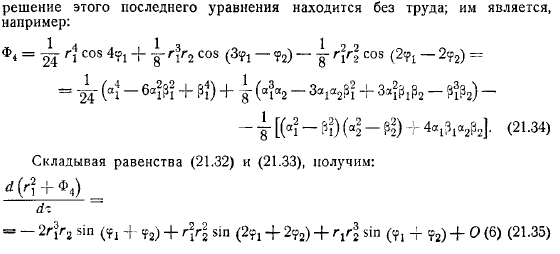
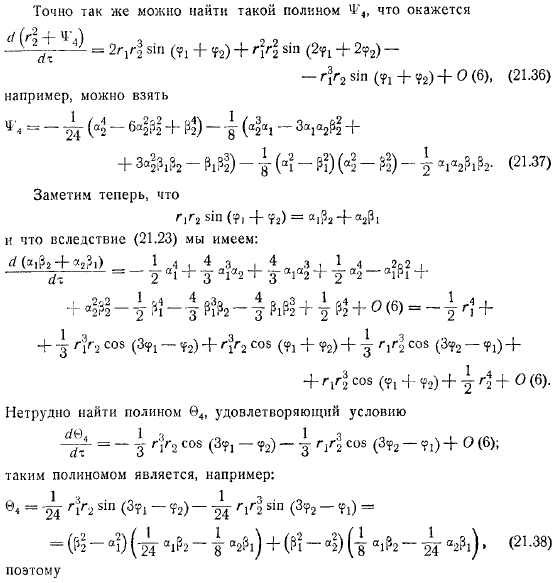
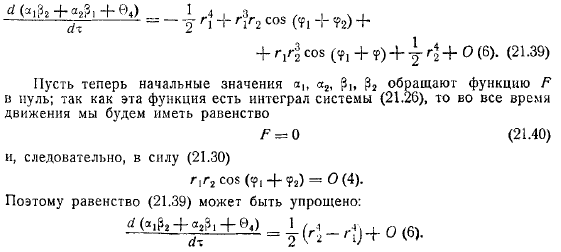




Об устойчивости вихревых цепочек Кармана
Создайте вихревую цепь кармана в гидромеханике. Под влиянием некоторых воздействий все или некоторые водовороты могут претерпевать небольшое смещение. После этого может оказаться, что вихрь течет. Если вы двигаетесь без движения, время, близкое к позиции будет. В этом случае говорят, что движение стабильно. Если смещенный вихрь удаляется от положения, соответствующего непертурбативному состоянию, его движение называется неустойчивостью.
- Используя это общее определение устойчивости, вы можете легко установить неустойчивость вихревой цепи Калмана без каких-либо. Дело в том, что если сместить цепи, например, все вихри в верхней цепи, на одну и ту же величину, то разница будет больше на эту величину, и только будет больше. Таким образом две вихревые цепочки , скорость всех вихрей обеих цепей определяется по формуле, требующей замены.
И понятно, что по крайней мере величина меняет свое значение, и поэтому все вихри движутся с небольшой, но постоянной скоростью из положения, соответствующего состоянию не возмущенного, и движение становится неустойчивым. Поэтому мы сужаем определение стабильности. То есть при небольшом смещении вихрей в начальный момент движение называется устойчивым, если расстояние между двумя вихрями в любой момент времени остается близким к расстоянию между этими вихрями в начальный момент.
Во-первых, мы доказываем неустойчивость вихревой цепи. Предположим, что на одинаковом расстоянии друг от друга вихри одинаковой интенсивности находятся на прямой. Разделите все эти вихри на группы. Группа четных вихрей и группа нечетных. Все вихри этот. Дайте такое же смещение и оставьте их на своих местах во всех странных вихрях.
До Кармана вихревую дорожку обнаружил Н.Е.Жуковский, при исследовании парадокса Дюбуа («О парадоксе Дюбуа», 1891). Людмила Фирмаль
Далее мы формируем цепочку из вихрей, расстояние между которыми составляет, соответственно, последовательных вихря. Движение этих вихревых цепей определяется по формулам. Если вычесть первое выражение из уравнения, то мы попадем на экватор если заменить все величины этого уравнения комплексными сопряженными, то получим: следовательно, заходим внутрь уравнения. Общий вид этих кривых показан на рисунке.
Положение равновесия вихря находится в его середине, то есть на пересечении линий семейства. Изолируйте область открытых или закрытых линий этого. Вихрь движется в область открытой кривой, он постепенно удаляется от вихря вдоль из этих открытых кривых. Если вихрь смещен в область замкнутой кривой, то он описывает замкнутый путь конечного размера, даже близкий к вихрю или, даже если начальное смещение вихря очень мало.
- Поэтому вихревая цепь неустойчива. Далее мы переходим к проблеме устойчивости вихревой цепи кармана. Разделите все вихри цепи на группы по вихря из каждой группы. Включите вихрь в основную группу и придайте смещение этим вихрям. Разделите цепочки на части. Состоит из вихрей, другой состоит из вихрей вихрь и вихрь. Как сумма термин, соответствующий каждой из цепочек: вместо присваивают этому выражению соответственно и отбрасывают термин схемы кармана движения тела в жидкости с образованием вихрей, который каждый раз уходит в бесконечность из рассмотрения.
Найти скорость цепи, например, для первого вихря. Затем дайте вихрю смещенные. To получив дифференциальные уравнения для этих перемещений, возьмем дифференциал левой и правой частей уравнения. Заметим, что в первый раз существует следующее значение аргумента синуса: в случае симметричного расположения цепей, в случае шахматной доски. Подставляя описательное значение аргумента в и группируя терм с, он выглядит так:для упрощения решения задачи да, делаем дополнительные предположения о характере смещения основного расположения вихрей.
То есть предположим, что величина смещения нечетного вихря одинакова, направление противоположное, а характеристики смещения четного вихря одинаковы. Легко видеть, что уравнение справедливо при этом предположении, и что уравнения совпадают соответственно. Таким образом, система из уравнений остается. Например, в первых выражения принимаются и могут быть преобразованы в тригонометрические функции с двойными углами.
Для симметричных массивов, для шахматной доски, для симметричных массивов, для симметричных массивов и действительные числа, а для шахмат действительные числа-мнимые. По последней формуле мы определили фактор. Это означает написать параллельное выражение симметричного расположения и шахматного расположения. Сначала перепишите. Расположение симметрии шахматное расположение далее опишем систему дифференциальных уравнений перемещения в ее действительном виде.
To сделайте это, введите следующее и отделите действительную или мнимую части последнего дифференциального уравнения. Получаем систему из следующих уравнений. Симметричный массив. Найти конкретное решение системы результатов линейных уравнений с постоянными коэффициентами в виде экспоненты. Постоянный. Создаем производную, присваиваем выражение выражению, а затем сводим все уравнения уравнения: симметричный массив, получаем систему алгебраических шашек.
Известно, что для совместимости однородной системы с уравнением определитель порядка должен состоять из коэффициентов. Это выглядит так: для симметричной компоновки и шахматного расположения. Корни этих уравнений имеют симметричное расположение, клетчатое. В случае порядка симметрии существуют определенные решения, содержащие функции. По мере увеличения смещение увеличивается, что делает движение неустойчивым. Для размещения шахмат вы получаете конкретное решение, которое содержит.
Экспонента с положительным показателем увеличивается с увеличением. Это указывает на нестабильность расположения в общем случае. Единственный случай, когда возможна стабильная работа — это обработка. Значение: это условие стабильности, полученное с помощью. Показывает связь между величинами, то есть расстояние между цепями и соседними вихрями каждой цепи. То есть, вы можете найти следующее приблизительное значение путем расчета. Это значение очень близко к данным, полученным в эксперименте по движению цилиндров в воде.
Указывает, что нестабильность движения достигается, даже если условие. To для этого необходимо провести более точное исследование, аналогичное тому, которое мы делали в начале разреза в случае единой цепи вихрей. Начните с системы уравнений и определите как функцию времени. То есть цепи вихря определяют движение всего. Уравнение предполагает, что цепочка вихрей без возмущений представляет собой скорость до обозначения, каждая из которых находится вблизи точки в начале.
Теперь предположим безразмерное смещение вихря в положении без возмущения как безразмерное время; уравнение принимает вид: следовательно, вычисляется в соответствии с начальным значением константы определения константы, причем последняя принимается такой, что эта константа устраняется, уравнение сохраняется на протяжении всего движения. То есть, если конкретно удовлетворяет равенству, а среднее расстояние между вихрями верхней и нижней цепей задается определенным случаем, когда выполняется условие Калмана, то предыдущая система имеет очевидный первый интеграл.
Расширьте с помощью ряда Тейлора: считайте вихревую цепь неустойчивой, если вы можете указать любое небольшое начальное смещение вихря, как показано в начале. Вы двигаетесь дальше, расстояние между двумя вихрями отличается от начального расстояния между этими вихрями на конечную величину. Очевидно, что неустойчивость цепи Калмана в случае выполнения условия доказывает, что сумма превышает конечное значение в дальнейшем движении, если она может указывать на какое-либо дальнейшее малое начальное значение.
Если оставить только член в правой части уравнения, то получится система первого приближения: если решить эту систему обычным способом, то получится чисто мнимых числа и даже алгебраических уравнения с двойными корнями. В этом случае будет указано, что для решения проблемы устойчивости необходимо учитывать всю систему. Для его изучения применяется метод Ляпунова. Введем, где непостоянный член равен порядку или больше. Первая приближенная система принимает вид, а первый интеграл.
Любая функция также является интегралом системы. В частности, обратите внимание на следующий интеграл: существует первый. Формула, для любого многочлена обозначает множество членов порядка наименьших. Затем запишите первое уравнение в виде: первые члена справа являются интегралами системы, помеченными. Теперь выберите полином, чтобы решение этого последнего уравнения можно было найти без проблем. Пример: добавление уравнения.
Аналогично можно найти полиномы, например: обратите внимание на следующее: в результате легко найти полином, удовлетворяющий следующим условиям: начальное значение, поскольку эта функция является интегралом системы, поскольку равенство получается во время движения целого, путем вычитания равенства: в конце добавьте функцию упрощения по предыдущим равенствам. В конечном итоге становится:из этого становится ясно, что существует неравенство для всех достаточно малых значений в определенной области, например.Вы получите итоговое значение бонуса.
По этой причине достаточно получить любые малые начальные значения, удовлетворяющие выражению и неравенству, и это, очевидно, можно сделать. Начальное значение функции обозначается через. Вот некоторые предположения по этому поводу. Тот факт, что сумма никогда не превышает значение, может привести. Факт, когда неравенство заполняется всем упражнением, выполняется, и в частности: функция уменьшается, так что во всем упражнении, но на протяжении всего времени упражнения, где положительное число, и выводя, увеличивается бесконечно.
Это противоречит тому факту, что полином должен оставаться ограниченным абсолютным значением области. Поэтому вы можете установить любое небольшое смещение вихря, чтобы расходиться на конечное значение, когда вихрь движется дальше. Это доказывает неустойчивость вихревой цепи Калмана и, в исключительных случаях, выполнение условий. Однако это последнее условие сохраняет некоторое значение, поскольку оно характеризует расположение вихрей, которое имеет наименьшую неустойчивость по сравнению со всеми другими вихревыми устройствами.
Он отметил ее как цепочку вихрей, образующихся при обтекании потоком воды плоской пластинки, установленной перпендикулярно течению. Людмила Фирмаль

