Оглавление:


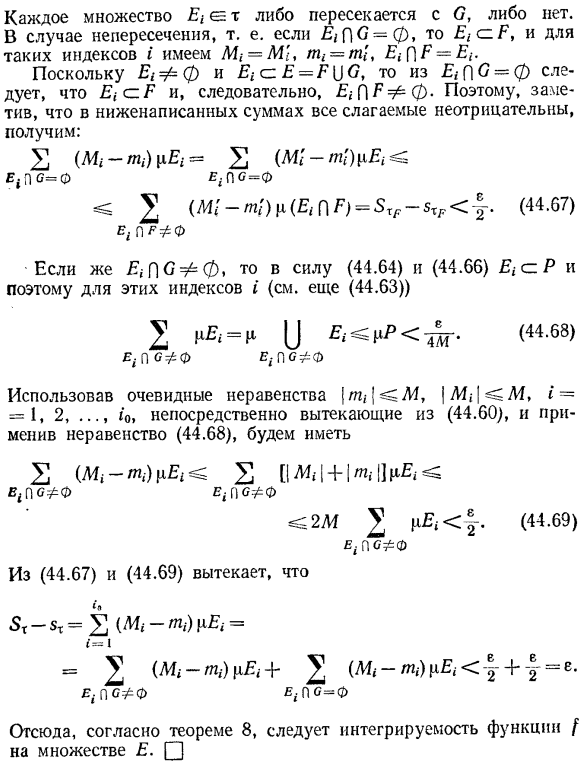

Об интегрируемости разрывных функций
Об интегрируемости разрывных функций. Непрерывность функций не является требованием интегрируемости.Существуют разрывные интегрируемые функции.Следующая теорема устанавливает разрывную интегрируемую функцию для достаточно широкого класса: Теорема 10.Доказательство.Определите функцию/и ограничьте ее компактным множеством, то есть ограниченным замкнутым множеством E C Pn.
Эта функция интегрируема по Риману, если функция ограничена измеримым компактным множеством Жордана, а мера Жордана для этого множества разрывов равна 0. Людмила Фирмаль
- Функция/ограничена существует, поэтому константа 0 0 существует, поэтому неравенство \ [(х)\ ^ м (44.60) Пусть Ao-множество функций / разрывов.Согласно гипотезе теоремы, если pD0 = 0, а следовательно, и фиксированный E0, то существует следующий ранг k: ^(ДОКСА-З ^ АГ-(44.61) Это, в данном случае, согласно определению、 Измерения, Hm p5y (Do)=0.Настройка с помощью многогранника 5 *(Do) к -► -} СО Детеныши (2б, 02).., 0r-куб, полученный из fu путем преобразования подобия вокруг центра Куба, представлен 0, коэффициент подобия равен 3;、 rD, = 3 » pO, / = 1, 2,…и./(44.62) Пять Пожалуйста, поставьте P-U Doo.
Благодаря неравенству(44.61) и (44.62)、 / = 1 Я 5 $ РД = Р II dx2U; = 2(Ор) з-44-63)/ = 1 / = 1 / = 1 Обратите внимание, что набор A является производным от 5 *(D0). ограничивая последнюю полосу Куба ребром длиной 10 —、 44.5.О интегрируемости дискретных функций Сто сорок три Набор, диаметр которого С1 (а) составляет менее 1 ч, которая пересекает установить 8 К (П) содержится в п (РИС. 172). d (A) 10 -*, A (] 8k (E0) φφ= R ΦA (44,64) Здесь обозначим через O множество внутренних точек многогранника 8k (E0).Очевидно, поскольку О является открытым множеством и замкнуто условием теоремы Е, то множество е = 7 также замкнуто.\ C также замкнут, и из-за ограничивающего характера E множество E ограничено;следовательно, P является compact.
- In кроме того, множество E0 находится внутри многогранника Zk (E0), то есть E0 и O (см.§44.1, как упоминалось выше). Это в целом верно для множества E и следует определению многогранника 8k (E)).Это означает, что функция/непрерывна в компактном множестве P и что множество I measurable измеримо как разность между 2 измеримыми множествами О и 0, а по теореме 9 функция / интегрируема в P.So для приведенного выше выбора e 0 будет 6 0 для разбиения xp в множестве P тонкости 6gr b, неравенство (44.65) Где 5X / Γ и$ xp-верхняя и нижняя суммы дарбу функции/, соответствующие разбиению tp П. Позвольте мне. 60 = tm {1(H, 6} (44.66) x = {D; K = D° мелкость 6X B0 множества e разделов.
Очевидно, что m / r = {гП ^ г, где E1 (] фффф) разбиение множества P тонкости 6X/, что хорошо, и, следовательно, по( 44.66), XP неравенство (44.65) стоит. Поставь Л4 * = Бир /(х), м(= м?/(Икс)、 / = 1 м \ = м! /(икс) х ^ Е ^ П ВР = е т р(Е1 [\ П). Е; ПР ^ Ф М1 = Бир /(х)、 х ^ Е ^ П 8 оп = е м ‘(\ х {Е1 {\ П)、 Е ^ РФФ 0 C 5X = y; m ID, 5X = y; t, rd §44.Кратные интегралы 144. Каждый набор либо пересекается с O, либо нет. Для непересеканий, то есть для E ^ 0-φ, с.Для такого индекса r, M1 = M ‘ 1, m1 = m [, E ^ P-E ^ С Esff и Яг. Если I = P O, то за ним следует ППО0-0 до C. I и, следовательно, ППП^ ^ фф.So.
В сумме, описанной ниже, мы получаем его, отмечая, что все термины неотрицательны. Людмила Фирмаль
- 2 (мг-/ у -) пно = ^(Λ1 «-/ ИГ) Е (ПС = е,.По = ф 2 (M / / и/) p (R ^ [] P)= 5 ^ 5Xp y. (44.67) Е. Для ППС ^ ^ φ, по( 44.64) и (44.66), CS. P, поэтому для этих индексов I (см. Также (44.63)) 2 =Я^ ^ ^ Ж^ (44.68) Е. по ^ ф Е4.По ^ ф Используйте очевидные неравенства в| / u / L4 in / M; / Л4, i = 1, 2, которые следуют непосредственно из (44.60)…Когда в точке 10 применяется неравенство (44.68) 、 2 (мг-г) М11 + / М1|] ПиДжей; EfOff ЕК [\выкл ^ 2 М 2 ^ Т (44-69) ЭФФФ (44.67) и (44.69) $ м-5Т = Д] (a4r по-Н) пно = = V (44r-n) Яг + + ((т) гг—| -4| = е. Ми., ПС № Ф Е. П С-Ф По теореме 8 это означает интегрируемость функции/на множестве H.
Смотрите также:
Решение задач по математическому анализу
| Определение кратного интеграла. | Свойства кратного интеграла. |
| Существование интеграла. | Критерии интегрируемости функций Римана и Дарбу и их следствия. |

