Оглавление:





Нормальные напряжения при внецентренном сжатии (растяжении)
- Например, давление от балок перекрытия на крайние колонны здания, давления от подкрановой балки на колонну, давление от балки колонны, давление от балки колонны, давление от балки колонны, давление от балки колонны давление от балки и т. д. в этом случае, в отличие от центрального сжатия в прямой балки (колонны), кроме продольного (обычного) внутренних сил, возникает изгибающий момент. Таким образом, внешнее сжатие (растяжение) является разновидностью деформации прямой балки, когда в ее
поперечном сечении одновременно действуют продольные сжимающие (тянущие) силы и изгибающие моменты. В этой главе мы рассмотрим стержень со значительной жесткостью на изгиб,который называется жесткостью. При расчете жесткости стержня отклонение (смещение) перпендикулярно продольной оси (стержня) от изгибающего момента не учитывается. Для риса. На рис. 23.1, а показан жесткий стержень, к которому в верхней
части приложена продольная сжимающая сила F в точке B. точка приложения силы G Людмила Фирмаль
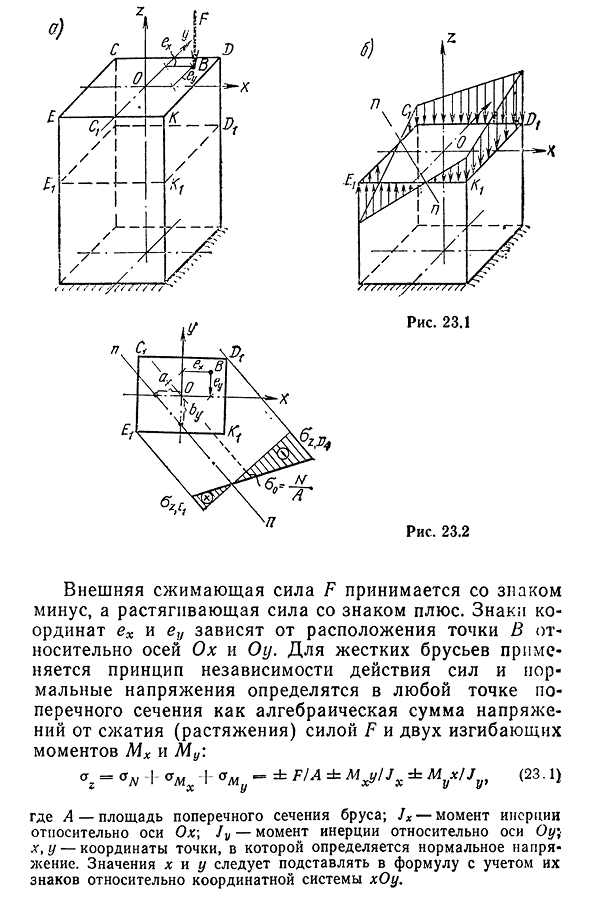
называется центром давления или полюсом. Точка B, в которой приложена сила F, так что она находится относительно главной центральной оси инерции Oh и координат Oh ex и EU, называется эксцентриситетом этих осей. От приложенной силы в любом поперечном сечении балки возникают два изгибающих момента для нормальной силы N= — F и главной оси Oh и Oh Mx= — Fey, My= — Fex. Семнадцать.* 259 стр. 23.2 Внешняя сжимающая сила, F, является знаком минус, а растягивающая сила-знаком плюс. Знаки координат ex и EU зависят от расположения точек, связанных с осями Oh и Oh. Для жесткого стержня применяется принцип независимости действия силы, нормальным напряжением является сила F и два изгибающих
момента MX и Mu\%=+ ° MX+°mu=±FIA±M^/J x±m yx lJ y,<23■ Где a-площадь поперечного сечения стержня, а Jx-момент инерции вокруг оси Ox, а момент инерции вокруг оси oy\x, y-значение x n y точки, определяемое нормальным напряжением, необходимо подставить в уравнение с учетом знака для HOU. В случае 260 В Центра внешнего сжатия(растяжения), когда точка приложения внешней силы F находится на главной оси инерции (например, на оси Y El==0), формула для определения нормального напряжения выглядит следующим образом:: og= = ±F / A±MX y! J x,(23.2) Бруски (прямоугольники, двутавровые балки и др.) с простой формой поперечного сечения.), При определении максимального
- нормального напряжения вычисляется значение напряжения числа точек, наиболее удаленных от осей координат. В этом случае участок строится аксонометрическими методами. Благодаря своей конфигурации значения напряжений в характерных точках расположены перпендикулярно плоскости поперечного сечения и соединены прямой линией(рис. 23.1, 6). При произвольной форме поперечного сечения для нахождения опасной точки определяется положение нейтральной оси, от которой находится наиболее удаленная точка, и создаются максимальные вертикальные
растягивающие и сжимающие напряжения. Уравнение нейтральной оси получается путем выравнивания нормального напряжения og до нуля: ±F / A±Mx u J J x±My x j y-0, (23.3)где xQ и Uo-текущие координаты точки нейтральной оси. Подставляя значения изгибающих моментов Mx=Fey и My = Fex в уравнение (23.3 ■ ■ ±Ф/а±Фэй г J х±фекс хо / Дж г- = о Или ±F/A (1+EU y^I x!A — / — ex J x J Y IA)+0. Уравнения ix=Y Jx/A и iy=Y Jy / A представляют собой радиус инерции поперечного сечения относительно главной центральной оси инерции Oh и Oh. Итак, как это±/?/A=^=0, в итоге получаем уравнение нейтральной оси в виде: 1+%J’O/ ‘ x+e xXO / ^=0-(2 3L ) Полученное уравнение является уравнением прямой, так как значения координат Lo и yQ имеют первую степень.
Нейтральная ось смещенного от центра сжатия (растяжения) не проходит через пересекающийся центр тяжести 261 Людмила Фирмаль
секция, от, go=; / o=O, oz^0. Чтобы определить положение нейтральной оси (нулевой линии), найдите отрезки, вырезанные этой осью на координатных осях Oh и O//. Давайте покажем эти сегменты с помощью Ah и Yy. Во-первых, найти значение отрезка ah, отрезанного нейтральной осью на оси Ah. Координаты пересечения нейтральной оси и оси ox равны xQ=ax и OO=O, а уравнение (23.4) принимает вид: Для определения отрезка U, подставляя уравнение (23.4), используя координаты OU Uo=U и XO=O оси пересечения нейтральной оси, получим l+Eby / ix2=0. Решая эти уравнения, получаем отрезки, которые разрезаются нейтральной осью на координатных осях: a x= — ‘ RCS и B y= — <23■5 ) Поскольку радиус инерции всегда положителен, значения Ah и ex, а также BU и EU имеют разные знаки. Таким
образом, точки действия нейтральной оси и внешних сил расположены напротив центра тяжести сечения. Положение нейтральной оси зависит не от величины и знака, а от координат точки приложения внешней силы F. После определения положения нейтральной оси перейдите к эпюре ОЗ. Для этого на контуре поперечного сечения, где находится наиболее удаленная от этой оси точка, рисуются две касательные, параллельные нейтральной оси. Это будет объяснено. 23.2, опасными точками будут D и E. Среди них вычисляются обычные напряжения D и O2) e, причем следует отметить, что полученные значения осаждаются по соответствующим касательным и при Сверхцентровом сжатии
(растяжении) нормальное напряжение в центроиде сечения всегда равно AG, o=±L^ / L. Расчет интенсивности пучка пластического материала при внецентровом сжатии (растяжении) основан на наибольшем (абсолютном) значении вертикального напряжения az, которое возникает наиболее далеко от нейтральной оси точки поперечного сечения.) Это будет объяснено. В точке 23.2, точка£>, условие прочности предельного состояния записывается следующим образом 262U2D=4-M x yD IJ x+My xD Y y\<Ry, (23-6)GDG a’D и координаты точки сечения, наиболее удаленной от оси d-Y-го
тролля;ry-расчетное сопротивление материала растягиванию(сжатию). Для стержней из материалов с различной устойчивостью к растяжению и сжатию проверьте прочность как при максимальном удлинении, так и при максимальном сжатии в точках нормальных напряжений E и D. Интенсивность внецентрового сжатия описывается двумя неравенствами: Наиб «» °Г, Е — ~+Мию/J х+м у Х е!Дж г<#р;1Д=°зд= — я-МХ ярдов/J х-моя хD у г<ПДУ,Дж (23.7) Где/?Rc-это расчетное сопротивление материала сжатию.
Смотрите также:
Решение задач по технической механике
| Расчет балок на прочность при косом изгибе | Ядро сечения |
| Прогибы при косом изгибе | Устойчивость центрально-сжатых стержней. Общие положения. |

