Оглавление:






Нормальные напряжения при плоском изгибе прямого стержня
- Нормальное давление Прямой гнуть адвокатского сословия плоский Рассмотрим случай чистого плоского изгиба балки (рис. 235, а). В общем случае изгиба из шести внутренних силовых факторов, которые могут действовать на это поперечное сечение, в чистом изгибе только изгибающий момент M отличается от нуля. Ось балки деформируется в плоскости, совпадающей с силой (см. 235-в плане чертежей). § 17 определил необходимые условия для того, чтобы изгиб был плоским. Этот параграф посвящен выведению формулы для расчета напряжений в любой точке раздела. До сих пор
мы не накладываем никаких ограничений на форму и положение силовой плоскости(за исключением того, что силовая плоскость не должна Двести тридцать пять Двадцать семь л Он проходит через ось стержня). Согласно общему плану/(§ 26), мы начинаем заключать путем рассмотрения- GP В нем содержится информация о проблемах Рении. Поперечное сечение x на любом расстоянии от начала координат (рис. 235, а). Рисует оси y Потратить на ГП Таким образом, в плоскости этого сечения 235 и g: ось y совместима с силовой линией (линией пересечения силовой плоскости и плоскости сечения), а ось g рисуется на любой высоте, но перпендикулярно оси Y. ось x направлена перпендикулярно плоскости поперечного сечения. Да
вайте выберем элементы площади DF в разделе которых Людмила Фирмаль
координаты Y и G. В целом, подчеркиваю, O и T могут действовать на элементы. Однако при чистом изгибе все силы и моменты, связанные с касательным напряжением (Qu, Qz, L4kr), равны нулю. Исходя из Формулы (3.29)—(3.34), можно предположить, что тангенциального напряжения в сечении нет, только сила, действующая на элемент DF adF=dN. Так… — QZ и^к п б) Из всех формул 240му(3.29) — (3.34) останется только три: Но в этом случае на сечение балки действует только один момент, поэтому L’=0; Mu=0; Mg=M. Из зависимостей(10.1)и(10. Два.) Рассмотрим изображение того же варианта луча(рис. 236). Эксперименты с упругими (например, резиновыми) моделями показывают, что при
расположении на поверхности модели прямоугольной сетки линий, позволяющей легко получить значительные деформации (236, а), деформируются путем чистого изгиба(рис. 236, б) следующим образом: а) продольные линии изогнуты по дуге. б) профиль поперечного сечения плоский. В) линия профиля поперечного сечения пересекает продольные волокна под прямым углом. Исходя из этого, при чистом изгибе можно предположить, что поперечное сечение балки остается плоским и вращается так, что оно удерживается перпендикулярно изогнутой оси балки. Однако гипотеза о плоском сечении с чистым изгибом, а также растяжением (сжатием) и скручиванием круглых стержней будет верной. Измеряя расстояние между контурными сходствами любых двух сечений, мы можем обнаружить, что эти расстояния изменяются во время
- деформации. Таким образом, a(рис. 236, Си б). Это означает, что верхние продольные волокна пучка будут короче, а нижние — длиннее. Однако также можно найти такой порт, длина изгиба которого остается неизменной(A0-a). Плотность волокна, которая не изменяет своей длины при изгибе балки, образована нейтральным слоем (НС). Волокна, принадлежащие нейтральному слою, до деформации находятся в одной плоскости, а в деформированном состоянии образуют цилиндрическую поверхность. В каждом случае каждое поперечное сечение пересекается с нейтральным слоем прямых линий, называемым нейтральной линией сечения (nl). При плоском изгибе нейтральный слой перпендикулярен силовой плоскости, что означает нейтральную линию 241º к линии силы
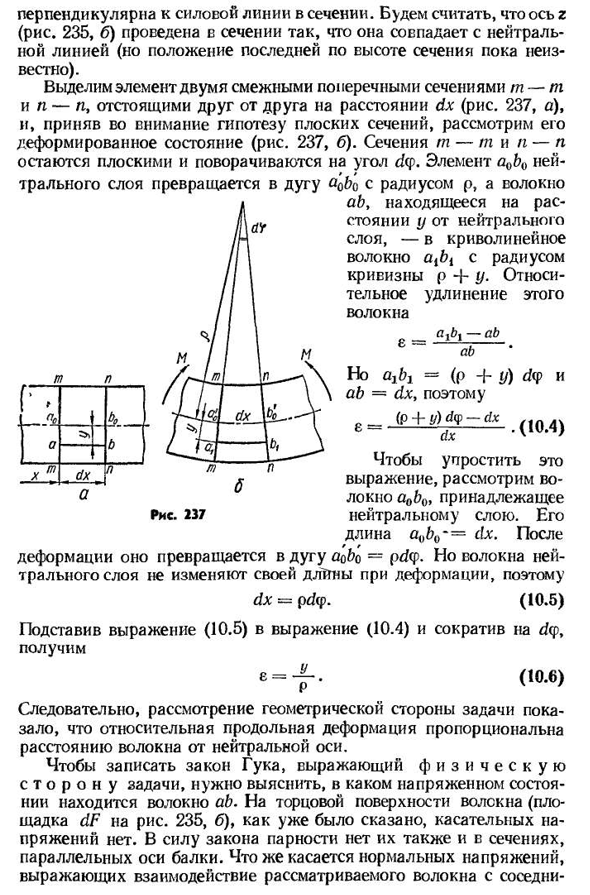
в поперечном сечении. Предположим, что ось Z(рис. 235, б) рисуется в разрезе в соответствии с нейтральной линией (но положение последней на высоте разреза до сих пор неизвестно). Выделите элементы по двум смежным участкам t-t и p-p, отстоящим друг от друга на расстоянии dx(рис. 237, а), и, рассматривая гипотезу плоского сечения, рассмотрим его деформационное состояние(рис. 237, б). Сечения t-t и p-p остаются плоскими и вращаются под углом d (f. элемент a0 ′ 0 радиус нейтрального слоя p и дуга a’ob’u будут иметь, волокно ab, расположенное на расстоянии y от нейтрального слоя, кривизну p4- Отчет _d Д-АВ Но ajbi=(p+»/) потому что dq>и ab=dx £= = (Р+^Ф-запроса (104) Чтобы упростить это выражение, рассмотрим волокно y0y0, которое принадлежит нейтральному слою. Его длина равна a (D-dx.
Но так как волокна нейтрального слоя не изменяют своей длины при деформации, Людмила Фирмаль
dx=pdcp. (10.5) если вы назначаете выражение (10.5)выражению (10.4) и уменьшаете его на dcp Е= — Ф-(ю. 6) таким образом, рассмотрение геометрических аспектов задачи показало, что относительная продольная деформация пропорциональна расстоянию волокон от нейтральной оси. Чтобы записать закон крючка, задачи f и z и h E S K u s t o R o n u, необходимо знать, в каком напряженном состоянии находится волокно ab на торце волокна (DF pad на рисунке. 235,6) как уже упоминалось, тангенциального напряжения нет. Согласно закону четности, они даже не существуют в частях, параллельных оси луча. Для нормального напряжения, которое представляет собой взаимодействие рассматриваемого волокна с соседним волокном、- 242-метровое волокно предполагает, что волокна не давят друг на друга, и поэтому эти напряжения равны нулю. Таким образом, волокно АВ находится в линейном
напряженном состоянии и испытывает простое растяжение или сжатие. Для этого он будет записан как закон крюк Я u ! = £10,7 •) Передача его в C и n t E z u исключает e из формул(10.6) и(10.7). О= (10.8) Подставляя зависимость от третьего выражения(10.8) (10.3), можно предположить, что E и p могут быть приняты как значения, не зависящие от положения элемента dF в разрезе в качестве знака интеграла.、 Е П ф г * ДФ=М. Ф Jt / M f=JZ представляет момент инерции трения о ось se — g G напоминает нам, что мы можем написать последнее уравнение 1М P EJZ’ (10.9) Наконец, если вы замените выражение (10.9) на выражение (10.8)、 (10.10)) Это
искомая формула, позволяющая рассчитать нормальное напряжение при чистом изгибе балки в любой точке ее поперечного сечения. Остается только установить, где в разрезе находится ось G, являющаяся нейтральной линией сечения. Чтобы ответить на этот вопрос, добавьте значение o формулы (10.10) к первым двум уравнениям(10.3): −4^[Y<#0;~(yzdF=0. От#=?* От 0, Ф ФРМ*=Ы J в yzdF — F F F Это Sr=0;(10.11) J^=0. (10.12) На основании равенства 241 (10.11) находим, что ось G нейтральной линии поперечного сечения является центром тяжести поперечного сечения (c. t. To сделать вывод, что он проходит). Силовая плоскость проходит через ось балки, что означает, что силовая линия(ось»/») проходит через центр тяжести
сечения. Знак равенства (10.12) указывает, что оси y и g являются главными центральными осями сечения. Он определяет положение линии нейтрального сечения. Таким образом, если силовая линия совпадает с одной из главных центральных осей сечения, то изгиб будет плоским, а нейтральная линия сечения совпадет с другой главной центральной осью. Другими словами, если плоскость силы совпадает с одной из главных Двести тридцать восемь Нейтральный слой совпадает с другой главной плоскостью. Заметим, что показатель степени z в обозначении момента инерции часто опускается. Теперь давайте проанализируем результаты. Формула для вывода(10.9) была вспомогательной, но она имеет большое
независимое значение. Поскольку речь идет о деформации (кривизне нейтрального c l o i^ — j с моментом, действующим на сечение), то ее можно интерпретировать как закон крюка в изгибе. Изделие EJ называется жесткостью изгибаемой части, КГЭ * см2. Из Формулы (10.9) следует, что если балка выполнена из однородного материала (E-const) и имеет определенное поперечное сечение (J-const), то при чистом изгибе (M=const) ее ось искривляется по дуге окружности. Формула (10.10) показывает, что независимо от формы и размера поперечного сечения напряжение в точке нейтральной линии равно нулю. Значение O линейно возрастает по мере удаления от нейтральной линии. В этом случае напряжение является
постоянным по ширине сечения (вдоль линии y-const). Таким образом, участок О любого сечения с горизонтальной осью симметрии всегда будет иметь вид, показанный на рисунке. 238 все волокна, расположенные над нейтральным проводом, сжимаются и растягиваются под ним. Если изгибающий момент имеет противоположный знак, верхние волокна растягиваются, а нижние волокна сжимаются. 244 наибольшего значения (omax) напряжения достигает случай симметрии поперечного сечения относительно горизонтальной оси G волокна, т. е. y=± — y, которая наиболее удалена от нейтральной линии. Подставляя это значение в уравнение (10.10),
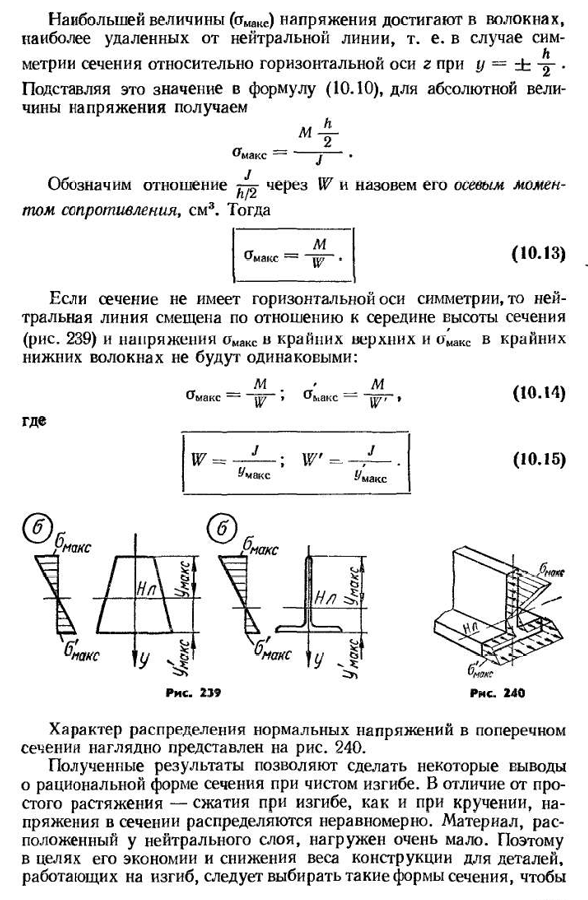
находим абсолютное значение результирующего напряжения Ч-м2 Бонус j • Он показывает отношение через-W, и его называют осевым моментом сопротивления, см3. Затем (10.13) Если сечение не имеет горизонтальной оси симметрии, то нейтральная линия смещается к центру высоты сечения (см. фиг. 239) и напряжение тока omax на весьма верхней части и Omax на весьма Нижнем волокне нет этого же: М (10.14) Samake-S. H. AKS=’ Распределение нормальных напряжений в поперечном сечении показано на рисунке. 240.
Смотрите также:
| Расчет винтовых цилиндрических пружин | Касательные напряжения при изгибе |
| Концентрация напряжений при кручении | Расчет на прочность при изгибе |

