Оглавление:




Нормальные напряжения при косом изгибе
- Нормальное напряжение при косом изгибе косой изгиб — это вид изгиба, при котором рабочая поверхность полного изгибающего момента в поперечном сечении не совпадает ни с одной из главных осей инерции поперечного сечения. Косой изгиб происходит в балках с прямой осью из-за несогласованности линии действия внешней нагрузки(силовой линии) с какой-либо главной центральной осью инерции. В этом случае силовая линия проходит через центр тяжести поперечного сечения балки. Если все внешние силы находятся в одной плоскости, происходит плоский косой изгиб. В этом случае упругая линия балки представляет собой плоскую кривую. Если нагрузка расположена в разных плоскостях, то в балке возникает
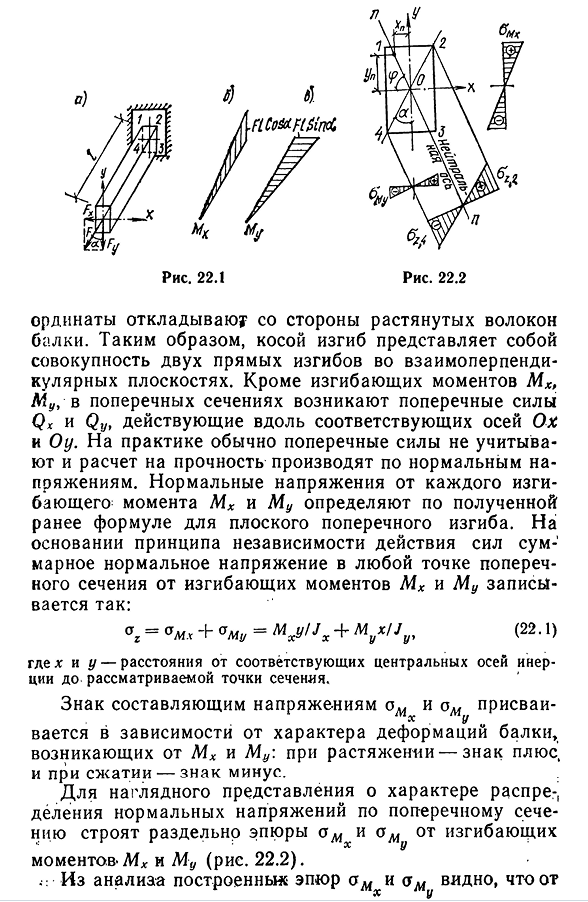
пространственный косой изгиб, а упругая линия-пространственная кривая. Исследовано явление плоского косого изгиба. В качестве примера рассмотрим консольную балку, нагруженную сосредоточенной силой F, которая направляет угол A в осевом направлении, учитывая, что силовая линия проходит через центр тяжести сечения(фиг. 22.1, а). Сила F разлагается на составляющие в направлении центрального шпинделя Oh и Oh. Fy = Feos a, Fx = F sin a. Компоненты Fy и Fx вызывают поперечный изгиб балки относительно осей oh и Oh. Изгибающий момент MX и Mu в любом сечении на расстоянии g от свободного конца балки будет равен: =FyZ=ФЗ потому что, МЮ=валютном з=ФЗ грех.
Обычно график изгибающего момента строится осесимметрично: график Людмила Фирмаль
вертикальной плоскости yOz mx и график горизонтальной плоскости hog Mu — (рис. 22.1, 6, б). Признаков сюжета MX и Mu не показывают, а 251 страница 22.2 Вертикальная ось откладывает^со стороны растянутых волокон пучка. Таким образом, косой изгиб-это совокупность изгибов двух прямых линий в плоскости, перпендикулярной друг другу. Кроме изгибающего момента MX, Mu, в поперечном сечении существуют поперечные силы Qx и Qy, действующие вдоль соответствующих осей Oh и Oh. На практике поперечная сила обычно не принимается во внимание, и расчет прочности проводится по нормальному напряжению. Нормальные напряжения от каждого изгибающего момента MX и MU определяются уравнением поперечного изгиба, полученным ранее. Исходя из принципа независимости суммы — » сечение изгибающего момента M X и нормального напряжения Mar в любой точке Mu
записывается следующим образом:=°MX+°mu=Mxy!J x+V / 7< / ‘(22-O Где x и y-расстояния от каждой центральной оси инерции до рассматриваемой точки поперечного сечения. Знак компонентного напряжения присваивается Омам и Омам в зависимости от характера деформации балки, возникающей в результате MX и Mu. Для наглядного выражения характера распределения нормальных напряжений по поперечному сечению отдельно составлены диаграммы»Qi-o-t изгибающий момент» MX и Mu(рис. 22.2). . : Из построенного графика анализа x и am y, то вы можете увидеть его Максимальное растягивающее нормальное напряжение в пределах 252 при совместном действии MX и MU заданного прямоугольного сечения изгибающего момента возникает в точке 2, а максимальное сжимающее напряжение-в точке 4, отсюда и максимальное сжимающее напряжение. А2>1=МХ/Г Х+М ylW г.<В J^=-М Х / З х-М Г / Ш Г где W*и Вайоминг моменты сопротивления в сочетании с относительно осей Ох и Оу. Обратите внимание, что это утверждение применимо только к тем сечениям (прямоугольникам, двутавровым
- балкам, каналам и т. д.).), При этом крайняя точка является наиболее удаленной от центральной оси Ох и ох. В разрезе любой формы, когда крайняя точка не находится одновременно на максимальном расстоянии от оси, О, это неправильно. Для такого участка сначала определяют положение нейтральной оси (нулевой линии), то есть геометрическое положение точки, в которой общее нормальное напряжение O2 равно нулю. Вертикальные напряжения при косом изгибе и вертикальные напряжения при прямом поперечном изгибе прямо пропорциональны расстоянию до нейтральной оси точки, поэтому максимальное вертикальное напряжение пропорционально расстоянию от нейтральной оси. Уравняв общее нормальное напряжение до нуля, получим формулу формулы нейтральной оси n-n: az=M xyn/Jx+MyXn/Iy=O, из которой — Up1x n-J * MVI JyMxt(22.2), где XP и y » — текущие координаты нейтральной оси. Из полученной формулы следует, что нейтральная ось представляет собой прямую
линию, проходящую через центр масс поперечного сечения. Чтобы определить его местоположение, введем следующее знаковое правило: возьмем положительное направление координатных осей Oh и Oh, а также вправо, и изгибающий момент MX и Mu соответственно в I сечении. В этом случае правая часть уравнения (22.2) положительна,и если знаки координат нейтральной оси CP и up различны, то уравнение удовлетворяется. 253 непрерывно нейтральная ось должна проходить через II и IV квадранты поперечного сечения. Обозначим угол наклона нейтральной оси к оси o через<p(рис. 22.2), то -Я не смогу этого сделать, — сказал он. said.Il джем.х,(22.3) В выражении(22.3), подставляя текущие значения изгибающих моментов консольных балок Mx=F zco sa и Afy=/
7zsina, получаем тг<Р=грех / Дж^С О С а=(QX в/дя)тг а, (22.4)где тг a-это тангенс угла наклона наклон линии действия силы до оси ОУ. Из Людмила Фирмаль
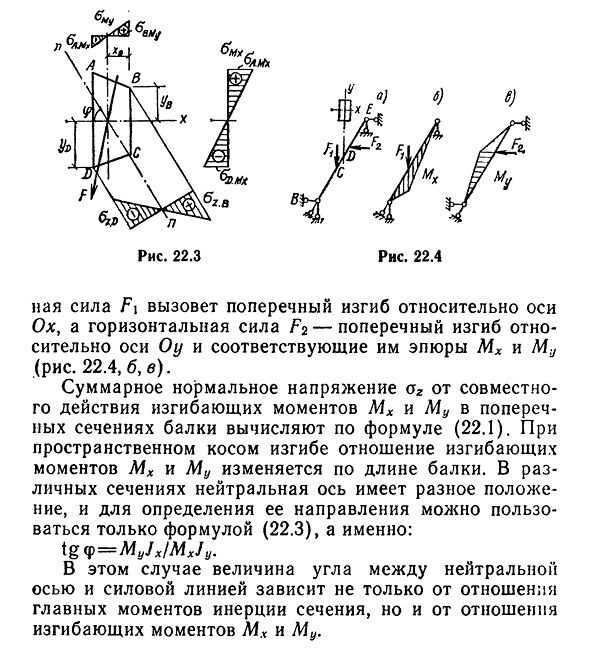
Формулы(22.4)видно,что в отличие от прямого поперечного изгиба при косом изгибе нейтральная ось не перпендикулярна силовой линии(tgcp^tga). Величина угла между ними зависит от отношения главных центральных моментов инерции к сечениям Jx и Jy. Только участки с Jx=J y (круг, кольцо, квадрат, равносторонний, правильный шестиугольник и т. д.). В этих участках угол между нейтральной осью и силовой линией составляет 90°, так как вся центральная ось является главной осью, и поэтому нет косого изгиба. Построим суммарный график нормального напряжения O2 для сечения, показанного на рисунке. 22.3. Проведите через центр тяжести нейтральную ось p-p по оси Oh параллельно углу CP, который находится на ней двумя касательными к сечению. В этом разделе
точки d и B не являются точками A, а находятся дальше всего от нейтральной оси. Перпендикулярно нейтральной оси нарисуйте ось графика O2. Величина вертикальной оси напряжения o2b и o2o соединены прямой линией. Пространственный косой изгиб происходит в балке под действием нагрузок, расположенных в разных плоскостях. Например, однопролетная балка с силой L, перпендикулярной сечению C, и силой F2, горизонтальной сечению D, испытывает пространственный косой изгиб(рис. 22.4, а). Действующая нагрузка может быть разложена на составляющие в направлении главной центральной оси инерции сечения, а также плоского косого изгиба. Затем эпюру изгибающих моментов МХ и Му. Пусть основные
центральные оси инерции Oh и Oh совпадают с направлением действующих сил F2 и F на рассматриваемую балку. Затем по вертикали- 254 страницы. Рис. 22.3. 22.4 Сила F\вызывает боковой изгиб относительно оси ox, а горизонтальная сила — вызывает боковой изгиб относительно оси OU, а соответствующие участки MX и Mu(рис. 22.4, б). Общее нормальное напряжение O2 от действия на соединение изгибающего момента MX и Μ в поперечном сечении балки рассчитывается по формуле (22.1). В пространстве косого изгиба отношение изгибающего момента MX к MU изменяется по длине балки. Нейтральная ось имеет разные положения в разных сечениях, и только формула (22.3) может быть использована для определения ее направления: tg f= = = A1u/X / M X / y. В этом случае величина угла между нейтральной осью и силовой линией зависит не только от соотношения основных моментов инерции сечения, но и от соотношения изгибающих моментов MX и Mu.
Смотрите также:
Решение задач по технической механике
| Перемещения линейные и угловые. Дифференциальное уравнение изогнутой оси балки и его решение | Расчет балок на прочность при косом изгибе |
| Расчет балок на жесткость при изгибе | Прогибы при косом изгибе |

