


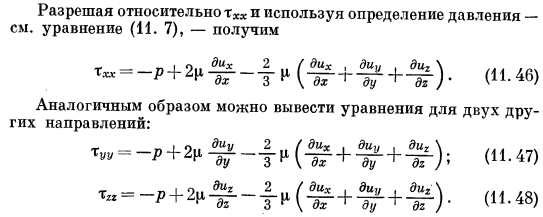

- Изучение нормального стресса несколько сложнее. Во-первых, определение (I. 7) по П〜(м * х 4″ Т1 / г 4-ти). В некоторых случаях, если жидкость неподвижна или движется так, что скорость привода одинакова, то каждое вертикальное напряжение численно равно в общем случае нормальное напряжение выражается как состоящее из фракции, обусловленной давлением, и фракции, обусловленной вязким напряжением, возникающим в результате продольной деформации текучего элемента в направлении этого нормального напряжения.
Сформулируйте это положение математически в виде (в направлении оси x спасибо = — p4th. (11.22) величина Р определяется по формуле (11. 17) уже решено. Формулу (I. 22) и использовать в комбинации. ^ х = tXx4-п; (11.23) ^ х-txx все Г(Txx4-М ^ 4-м»); (11.24) °х-УЗ «(Хыу 4-ТП) (11.25) Если разделить вязкое нормальное напряжениеy на 2 части, то формулу (I. 25) полезно преобразовать в следующий формат: = «Я»(txx все ~~ хуу)+ г ^ txx все м»).(11.26) Аналогично можно вывести уравнение U mx.
Формула (11. 22) путем подстановки уравнений Oxy, oy и o2 соответственно (I. 27),(I. 28), (11.29). Спасибо = — р 4-г(ТНХ-Туу) — (далее-СПС); (11. 27) (°) (б) (ы) = — р-г (т»-Туа)+(Туу _ ТВ). (1!28) (°) (Б) (а) Т » = — р + г(ти-ТН)—1 (Ти, Ти). (11.29) ( * ) © (о) под отдельными членами этих 3 уравнений обозначение (a), (6), ©, (d) затем используется в качестве удобного средства идентификации. Под действием нормального напряжения Txx происходит деформация в направлении оси X. — ^- предположим, что скорость деформации в направлении оси x может быть определена путем суммирования вкладов из членов, содержащихся в 3 уравнениях выше для нормального напряжения.
Во-первых, рассмотрим вклад давления в объем (обозначается изменением давления) Плотность элемента изменяется. Процент этого изменения выражается уравнением непрерывности Уравнение (9. 14) как показано, левая часть этого уравнения также равна скорости объемной деформации (растяжения). Поскольку давление во всех направлениях одинаково, вклад давления в скорость деформации в направлении оси x выражается следующим образом: / \ дичь 1 1 1 1(Дич 1 \ \ ДХ)3 VПх3 (ДХ 1 1 до 1 ДГ) (11.31) Уравнение(I. 27)-I.
- Остальные напряжения, которые входят в него, рассматриваются попарно (6, c, (I)). Выбираются таким образом, что выбранный элемент считается подвергнутым чистому сдвигу-если это может быть легко analyzed. In чистый сдвиг, элемент, который подвергается однонаправленному сжатию и вертикальному растяжению одинаковой величины, работает так, чтобы на него воздействовало только тангенциальное напряжение плоскости, наклоненной под углом 45°к оси. А касательная равна величине нормального напряжения, приложенного к элементу с внешней стороны X. Во-первых, формула 11.
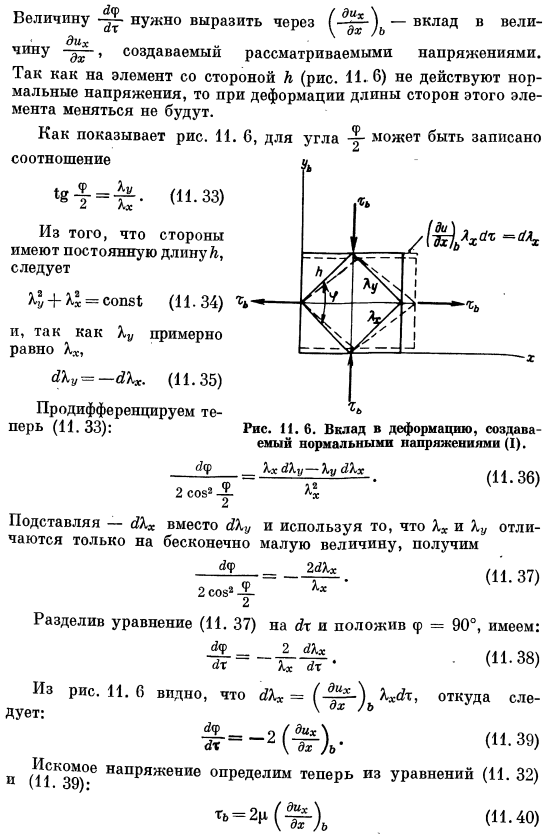
Рассмотрим термины, обозначенные индексом (b).Эти напряжения действуют, как показано на рисунке. И напряжение в направлении вдоль оси x положительное (растяжение), а напряжение в направлении вдоль оси y отрицательное(сжатие). в то же время напряжение сдвига xb пропорционально скорости угловой деформации. Е = —ч — ^ » = » 3 (txx все(11.32) 1. эти вопросы более подробно объясняются в обычном механическом руководстве. Например, см. [163]. Ров. Ранг-dx-создается напряжением задачи.
Поскольку элементы стороны k не подвержены воздействию нормальных напряжений(рис. 11.6), длина стороны этого элемента не изменяется при деформации. Как на фото. I. 6, угол-u Соотношение =(11-33) Так как стороны имеют постоянную длину/ г、 ^- /- =ωШ(11.34) потому что ku почти равно xx、 (И. Тридцать пять) Теперь различают(11.33): Рисунок 11. 6.Вклад в деформацию, вызванную нормальным напряжением (I). Это хорошо. ху-ху АКХ 2Х824 — с? Пользуясь тем, что вместо c1ku заменено на Xx, Ax и Hu отличаются только локальным минимумом、 (11.36)) НЧ 2 в COS 2 2 (11.37)) Уравнение 11.
Разделить на cp = 90°и установить следующим образом: ^ Ф = _ _ _ _ _ _ 2 ах АГ х а * (11.38) От Дующий: Рисунок 11.6 показывает, что1xx = * Φ_ 9 (\Дич * \ — ГД) б * Откуда SI 39) И Требуемое напряжение(I. тридцать девять): Определить из уравнения (11. Тридцать два) (11.40) и, наконец, (11.41) / Диг \ __ ХВ \ ДХ)2р. Или «* ■ » > Уравнение(I. 27)-(I. 29) из 4 включенных групп напряжений 2 уже были приняты во внимание. Снова определить вклад 3-й группы И d ^ 22 ″ ^ xx ^ «Гг» 7ого блока ^ 1 я 1 ″ ■1 1 Рис. 11.7.Вклад в деформацию, вызванную нормальным напряжением (I).
Его смещение, как показано на рисунке. I. 7. / вывод таким же образом, как dih\ Когда решать Диг \ _ 1 Спасибо-ХХХ ДХ / х 2р. Три (11.43)) Формула (I. 27)-(I. 29) пара оставшихся напряжений, отмеченных в индексе (Phi), не вызывает деформации в направлении оси X. То есть,= 0.Скорость деформации Направление x, вызванное нормальным напряжением, равно сумме скоростей деформации, рассмотренных выше dich 1 / dich. Диво. и Di2. 1 Спасибо-Туу, 1 ВХ-Чи = ’- dTL ’ — dG) 1 3 3 Или 1 1 МГП(МГП-1 ГУР 1 | ТНХ ТНХ + Туу + спасибо ДХ-3 ’(ДХ П У Н ДГ) 1 2П 2П-3 (11.45) решение относительно txx и использование определения уравнения давления (I. 7) см.、 Txx-p + 2c — ^ — | — (Ц.
Смотрите также:
| Уравнения в напряжениях | Уравнения Навье — Стокса |
| Уравнения движения в напряжениях | Ламинарное параллельное движение между плоскими стенками |
