Оглавление:



Нормальные и касательные напряжения при изгибе
- Нормальное и тангенциальное давление изгиба. Рассмотрение относительного порядка величины нормальных и тангенциальных напряжений изгиба, приведенного в § 101, не относится к тонкостенным стержням. Изгиб и кручение, возникающие в результате тангенциальных напряжений, таких как стержни
и та же цифра, что и нормальное напряжение, нельзя сбрасывать со счетов. Касательным напряжением изгиба мы называем напряжение, распределенное почти равномерно по толщине стенок профиля, не связанное с
закручиванием стержня. Например, если Людмила Фирмаль
симметричный стержень, по крайней мере двутавровая балка или канал, изгибается силой, действующей на его плоскость симметрии, то ясно, что никакого скручивания нет. Очень высокая жесткость В баре нет. Кручение замкнутых тонкостенных профилей делает для
них вопрос о вторичных ситуациях отсутствия кручения. В том же случае, даже если тонкостенный стержень открытого профиля изогнут в плоскости, даже если основная плоскость не является симметричной плоскостью, особенно для того, чтобы предотвратить скручивание, мы предполагаем, что при определенных
- обстоятельствах нет скручивания тангенциального тангенциального, поэтому другие напряжения не напрягаются при наличии напряжений в провисающем сечении, сдвигаются, то есть вызывают изменение исходного прямого угла. 187), так как сечение не может оставаться перпендикулярным изогнутой оси стержня, а напряжения в сечении распределены неравномерно. Однако, если к стержню приложена сосредоточенная нагрузка, то сила сдвига постоянна в каждом сечении, поэтому для всех сечений этого сечения
тангенциальное напряжение равно 276. Точно так же и искажение поперечного сечения такое же. Длина элемента TP между двумя участками после деформации равна»длине одного и того же элемента, вычисленной по гипотезе плоского участка»: то есть в m’ri концентрация элементов равна длине одного и того же элемента. Более точный расчет показывает, что влияние поперечного искаженияみ тангенциальным напряжением изгиба на распределение нормального напряжения в более общем примере потери нагрузки незначительно, поэтому уравнение (126.1) является общим. Чтобы найти касательные напряжения,
будем считать, что они распределены, но(рис. Толщина стенок равна-188). Людмила Фирмаль
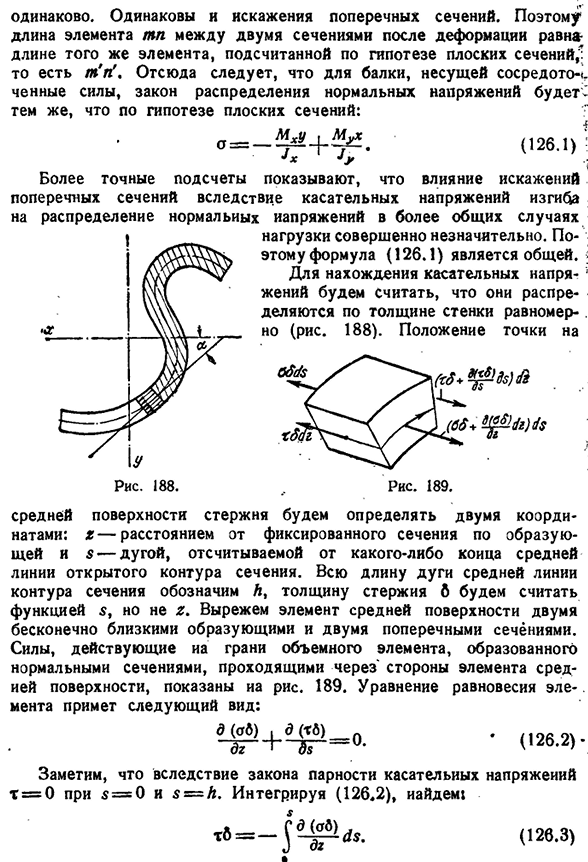
Положение верхней точки ■С Поверхность стержня определяется двумя координатами z-расстояние от неподвижного поперечного сечения на изображении y — $ — дуга, отсчитываемая от любого конца среднего значения Средняя крапива: щи и разомкнутая линия сечения. Общая длина дуги средней линии контура сечения обозначается Y, а толщина стержня B является функция, а не Г. Сила, действующая на поверхность объемного элемента, образованного обычным сечением, проходящим через стороны элементов средней плоскости, показана на рисунке. Уравнение равновесия 189
элементов принимает вид: — 3i-I-e g* — ° — по закону касательного напряжения, при t=0 s=0 и$=y. заметим, что интеграл (126.2), находим:. с- (126.2)- (126.3)§ 127] напряжение сдвига при изгибе 277 Но, согласно формуле (126.1), учитывая независимость b от g, получаем! <9 (OI) _6ydMx ■ bxdM, DG JX dz’Ju dz ’ запомните дифференциальное соотношение между изгибающим моментом и сдвиговой силой и запишите последнее уравнение следующим образом: Подставляя эту формулу в Формулу (126.3), получаем следующую формулу для закона распределения касательных напряжений: S Л — УБ Д С-Ф-в J2-ДС(126.4) * О. В Интеграл в Формуле (126.4) представляет собой статический момент некоторых заштрихованных участков на рисунке. 182.
Смотрите также:
| Продольно-поперечный изгиб | Касательные напряжении при изгибе в плоскости симметрии |
| Изгиб балки на упругом основании | Центр изгиба |

