Оглавление:
Нормальное уравнение прямой
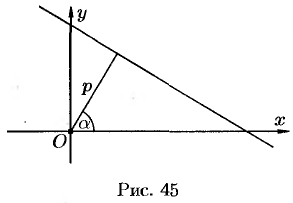
Пусть прямая определяется заданием 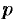 и
и 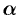 (см. рис. 45). Рассмотрим прямоугольную систему координат
(см. рис. 45). Рассмотрим прямоугольную систему координат 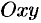 . Введем полярную систему, взяв
. Введем полярную систему, взяв 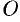 за полюс и
за полюс и 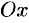 за полярную ось. Уравнение прямой можно записать в виде
за полярную ось. Уравнение прямой можно записать в виде
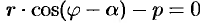 , т. е.
, т. е. 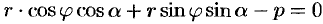 .
.
Но, в силу формул, связывающих прямоугольные и полярные координаты, имеем: 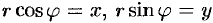 . Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид
. Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид
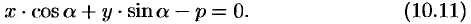
Уравнение (10.11) называется нормальным уравнением прямой.
Покажем, как привести уравнение (10.4) прямой к виду (10.11).
Умножим все члены уравнения (10.4) на некоторый множитель 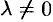 . Получим
. Получим 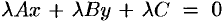 . Это уравнение должно обратиться в уравнение (10.11). Следовательно, должны выполняться равенства:
. Это уравнение должно обратиться в уравнение (10.11). Следовательно, должны выполняться равенства: 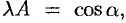
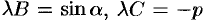 . Из первых двух
. Из первых двух
равенств находим
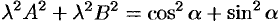 , т. e.
, т. e. 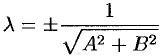 .
.
Множитель 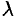 называется нормирующим множителем. Согласно третьему равенству
называется нормирующим множителем. Согласно третьему равенству 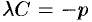 знак нормирующего множителя противоположен знаку свободного члена
знак нормирующего множителя противоположен знаку свободного члена 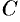 общего уравнения прямой.
общего уравнения прямой.
Пример №10.2.
Привести уравнение 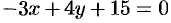 к нормальному виду.
к нормальному виду.
Решение:
Находим нормирующий множитель 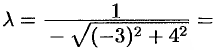
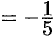 . Умножая данное уравнение на
. Умножая данное уравнение на 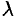 , получим искомое нормальное уравнение прямой:
, получим искомое нормальное уравнение прямой: 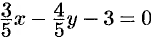 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору |
| Полярное уравнение прямой |
| Исследование формы эллипса по его уравнению |
| Дополнительные сведения об эллипсе |

