Нормальное уравнение плоскости

Нормальное уравнение плоскости

Положение плоскости 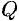вполне определяется заданием единичного вектора 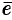, имеющего направление перпендикуляра 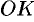, опущенного на плоскость из начала координат, и длиной 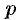этого перпендикуляра (см. рис. 71).

Пусть 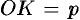, а 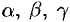— углы, образованные единичным вектором 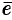с осями и 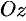. Тогда 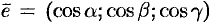. Возьмем на плоскости произвольную точку 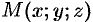и соединим ее с началом координат. Образуем вектор .

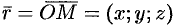При любом положении точки 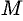на плоскости 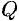проекция радиус-вектора на направление вектора 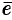всегда равно 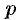: 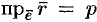, т. е. 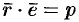или

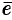Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов и , уравнение (12.8) перепишем в виде

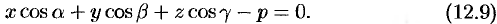
Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.

Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на нормирующий множитель 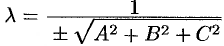, где знак берется противоположным знаку свободного члена 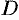общего уравнения плоскости.

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Уравнение плоскости, проходящей через три данные точки

Уравнение плоскости в отрезках

Эллипсоид

Однополостный гиперболоид