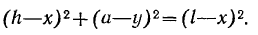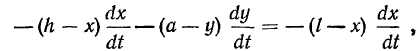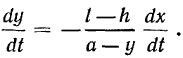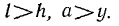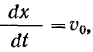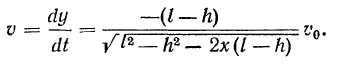Задача №1.
Нить 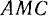 закреплена одним концом в неподвижной точке
закреплена одним концом в неподвижной точке 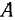 и продета через кольцо
и продета через кольцо 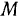 , скользящее с постоянной скоростью
, скользящее с постоянной скоростью 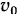 по неподвижному стержню
по неподвижному стержню  . Другой конец нити привязан к ползуну
. Другой конец нити привязан к ползуну 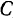 , скользящему по вертикальному стержню
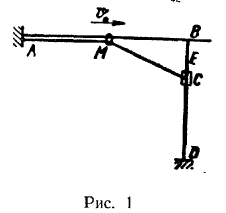
, скользящему по вертикальному стержню 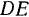 (рис. 1). Длина нити равна
(рис. 1). Длина нити равна 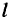 , расстояние
, расстояние 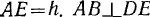 . Определить скорость ползуна
. Определить скорость ползуна 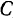 в зависимости от расстояния
в зависимости от расстояния 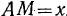 .
.
Решение:
Определим «положение точки 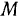 координатой
координатой 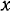 , определяющей расстояние точки
, определяющей расстояние точки 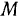 от точки
от точки 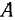 , а положение точки
, а положение точки 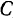 — координатой
— координатой 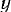 , определяющей ее расстояние от точки
, определяющей ее расстояние от точки 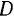 , Так как скорость точки
, Так как скорость точки 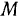 задана, то производная
задана, то производная
Для определения скорости точки 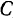 нужно сначала установить тождественную зависимость координат
нужно сначала установить тождественную зависимость координат 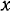 и
и 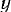 . Эта зависимость сразу следует из свойств
. Эта зависимость сразу следует из свойств 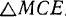 . Обозначим через
. Обозначим через 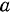 длину стержня
длину стержня 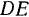 . Тогда
. Тогда
Это соотношение остается справедливым в любой момент времени и может рассматриваться как тождество по времени. Дифференцируя это тождество, получим
откуда сразу следует
Здесь
Исключая у и имея в виду, что
получим
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №2. Ползун приводится в движение вдоль стержня при помощи нити, продетой через неподвижное кольцо и наматывающейся на колесо, вращающееся с постоянной угловой скоростью (рис.-2). Определить скорость ползуна как функцию расстояния , если , а радиус колеса равен. |
| Задача №3. Ползун приводится о движение посредством нити, наматывающейся на шкив радиуса . Определить скорость ползуна в зависимости от расстояния , если угловая скорость шкива равна (рис. 3). |
| Задача №60. Прямолинейная трубка вращается в вертикальной плоскости вокруг горизонтальной оси с постоянной угловой скоростью . В трубке находится тяжелый шарик массы , прикрепленный к пружине, другой конец которой закреплен в точке . Найти закон движения шарика относительно трубки, считая упругую силу пружины пропорциональной ее удлинению с коэффициентом пропорциональности . В начальный момент трубка горизонтальна, а относительная скорость шарика равна нулю. Пружина в начальный момент имеет естественную длину . Рассмотреть случай. |
| Задача №61. Окружность радиуса , плоскость которой вертикальна, вращается вокруг своего вертикального неподвижного диаметра с постоянной по величине угловой скоростью . По окружности может свободно скользить тяжелая материальная точка массы . Определить положение относительного равновесия материальной точки и найти период малых колебаний точки около положения устойчивого равновесия. |

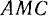 закреплена одним концом в неподвижной точке
закреплена одним концом в неподвижной точке 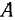 и продета через кольцо
и продета через кольцо 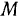 , скользящее с постоянной скоростью
, скользящее с постоянной скоростью 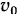 по неподвижному стержню
по неподвижному стержню  . Другой конец нити привязан к ползуну
. Другой конец нити привязан к ползуну 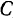 , скользящему по вертикальному стержню
, скользящему по вертикальному стержню 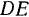 (рис. 1). Длина нити равна
(рис. 1). Длина нити равна 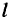 , расстояние
, расстояние 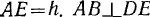 . Определить скорость ползуна
. Определить скорость ползуна 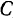 в зависимости от расстояния
в зависимости от расстояния 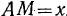 .
.
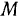 координатой
координатой 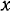 , определяющей расстояние точки
, определяющей расстояние точки 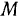 от точки
от точки 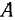 , а положение точки
, а положение точки 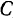 — координатой
— координатой 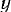 , определяющей ее расстояние от точки
, определяющей ее расстояние от точки 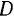 , Так как скорость точки
, Так как скорость точки 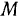 задана, то производная
задана, то производная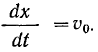
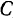 нужно сначала установить тождественную зависимость координат
нужно сначала установить тождественную зависимость координат 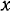 и
и 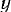 . Эта зависимость сразу следует из свойств
. Эта зависимость сразу следует из свойств 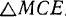 . Обозначим через
. Обозначим через 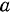 длину стержня
длину стержня 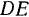 . Тогда
. Тогда