Оглавление:



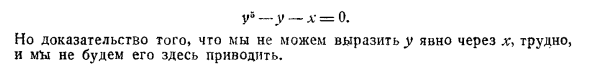
Неявные алгебраические функции
- Неявная функция алгебры. Это легко проверить если у = у * \ х-у \ = х т тогда / L + ^ V —0 + x? \ 1 -y) (1 -X) r 1 и у = VxL-Vx + Vx, тогда Y- (4y * -f4y + l) jC =: 0 Форма каждого из этих уравнений Где … Rm — рациональная функция от x. Простой читатель Если у — одна из функций, обсуждаемых в последней серии примеров, убедитесь, что у удовлетворяет этой форме уравнения.
Легко доказать, что это предположение верно, но мы не останемся здесь, когда проведем формальное доказательство. В следующем примере читатель может ясно увидеть, как проходит такое доказательство. Дай мне х + ух + ух + y- ‘■: ~ «s • x-yx + / x + yx-y \ ~ + ~ x тогда y = u + v + w X- и V-W ‘ tr = X, ZT = X -f- и »X,И то, что можно исключить из этих выражений, это v, w, которое получает выражение в нужном формате. Итак, мы приходим к следующему определению: y — алгебраическая функция от x порядка m, если она является корнем уравнения порядка m от y с коэффициентом, который является рациональной функцией от x.
Существует предположение, что это имеет место для явных алгебраических функций Людмила Фирмаль
Без ограничения общности можно предположить, что коэффициент старения, такой как (1), равен 1. Этот класс функций включает в себя все явные алгебраические функции, рассмотренные в и. 26. Однако включены и другие функции, которые не могут быть выражены как явные алгебраические функции. Это связано с тем, что в общем случае мы знаем, что уравнения, такие как (1), не могут быть решены явно относительно y. Тем не менее, такое решение составляет 2, 3, 4 или Особый случай, когда значение t велико.
Определение алгебраической функции следует сравнить с определением алгебраического числа и предыдущей главой (другой пример, 36). Пример XIV. I. m ~ > y — рациональная функция. 2. Для m = 2 формула уравнения ys — {- R & 4 Rs = v = ri {-? , ± uzr ^ n} • Эта функция определена для всех значений l-. # *> 4 /? Случай 2 имеет два значения: / ?? = 4 /? Случай 2 имеет одно значение. // Если 1 = 3 или 4, вы можете применить метод решения кубических и квартичных уравнений, показанный в алгебраическом курсе.
| Рациональные функции | Трансцендентные функции |
| Явные алгебраические функции | Графическое решение уравнений, содержащих одно неизвестное число |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Однако эти методы в принципе очень сложны, а результаты очень утомительны, поэтому в этих случаях удобнее изучать функции непосредственно с использованием исходных уравнений. 3. Рассмотрим функцию, определяемую уравнением y * -2y-l * 3 = 0, y2-2y -} — l-3 = 0, y * -2y8 + x * = 0, В любом случае найдите y как явную функцию от x. Указывает значение x, для которого определены эти функции. 4. Найти алгебраическое уравнение с коэффициентами, являющимися рациональными функциями от x, которые удовлетворяют v * + y ~ x-, V * + Vt ‘Y’x + Vx + yf. 5. Рассмотрим уравнение y4 га. [Где у2 = ± х. Если x положительный, y есть yx. Если x отрицательно, y = -x.
Следовательно, функция имеет два значения для всех значений x, кроме jc = 0. 6. Алгебраическая функция от x также является алгебраической функцией от x. [Это может быть доказано в основном по той же причине, что и на страницах 37 и 45 примеров 37 и 38. Не выходит из уравнения Ут + ф? I () Ut ‘1 + — • 4-f? () = 0, zn + S, (x) + … + Sn (x) = 0 n (ym + f? x (zh) ym-1 + … + Rm (2h) l Раздастся корень ж во втором выражении. ] 7. Вероятно, это должен быть еще один пример алгебраической функции, которая не может быть выражена в явной алгебраической форме. Примером является функция y, определяемая уравнением.в 5 y _ d. _ 0.
Однако трудно доказать, что q нельзя выразить явно в q, поэтому здесь это не объясняется. Людмила Фирмаль

