Невырожденное нормальное распределение

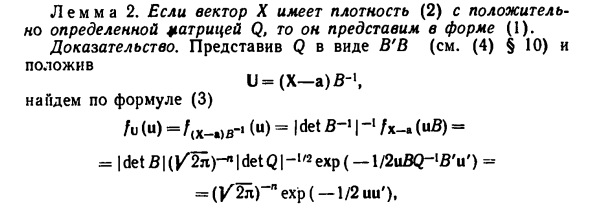
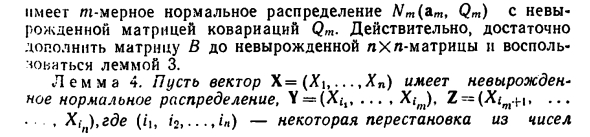
Невырожденное нормальное распределение

• U \ с плотностью распределения ф (*) = = е- * ч2 / уг2я называется стандартной. Сл. в. Xi = oU \ + n имеет цифровой а «‘ф ((х — ц) / а) общего нормального закона # (ц, а). Связь между U \ и Х \ послужила нам отправной точкой для введенного осуществление многомерного нормального распределения. Определение 1. Стандартным нормальным случайным век- вектором назовем вектор V = (UuU2t. .., Un) из независимых стандартных нормальных компонентов. Вектор U имеет математическое ожидание 0, матрицу кова- риаций /, его выделение обозначено N „@, /).

Определение 2. Пусть а = (аи а2, …, а) -ожидаемый числовой вектор, В = \ Ьц, i, j = l, …, n] -невырожденная число- числовая матрица. X = UB + a, A); где U-стандартный нормальный вектор, назовем невырожденного невырожденным п-мерным нормальным распределением. Лемма 1. Нормальный вектор X, установлен формулой А), имеет математическое ожидание л, матрицу ковариаций Q = -В’В и числовое распределение вероятностей -a) Q — ‘(x-a)’). B) Соказательство. C)

Преобразование плотности справедлива при любом распределении вектором U. Людмила Фирмаль

Действительно, взяв А = {х: xi <; al, …, Xn <an} и ис- используя замену значения x5- ‘= U, запишем f f | det5 | — ‘/ u (x5-1) dx1 … dxn = f f / u (и = P (U e ЛВ- ‘) = P (U5e A), т. е. ф. р. РА15еЛ) в UB представлены как л-мерный ин- 101 по множеству следовательно, является плотностью распределения по траектории 115. Воспользуемся формулой C), заметив, что аналог рас- распределение векторов U в A) равно / и (и) — / „, (и,) … fvn (« „) = (/ §?) — exp (-1 / 2 ии). D) В результате получился формулой Б) пои а = 0. Переход к случаю а ^ = 0 не вызывает затруднений. 1.ледствие 1.

Если матрица о ортогональна: В’В = 1,. То вектор X, определенный формулой A) при а = 0, имеет распред регистра; VH @, /). Следствие 2. Функция f (x), заданная формулой B) при Q, является плотностью некоторого нормального вектора X. Действительно, представив Q в виде В’В, где 5-невырожденная матрица (см. D) § 10), тре- требуемый вектор X можно определить по формуле A) с данными В и а. ¦ Таким образом, можно дать эквивалентное определение л-мер- распределенного распределения распределением с плотностью B). а положительно определенная матрица Q-матрицей ковариа- цнн этого распределения. Q). Ш

• Отметим частный случай двумерного невырожденного нор- нормальным распределением в виде 2р я О, его матрица ковариаций равна Лемма 2. Если вектор Х имеет значение В) с положитель- Q, чтобы он был представлен в форме A). Показательство. Представив Q в виде В’В (см. Д) § 10) и положив U = (X — а) ,, найдем по формуле C) / и (и) = / (Х ,) В-. (и) = | дет 5- ‘| -‘ / х-а (иВ) = = | det5 | (/ 2ll) -n | detQ | -l’2exp (—l / 2u5Q-lBV) = 102 так что вектор имеет распределение М „@, /), а Х выражается через него по формуле А). В следующей лемме, а также всюду отмеченный нижним индексом матрицы.

Лемма 3. получается вычеркиванием из всех, строк и столбцов с номерами, отличными от i’i, •••. ‘* • В ча- в частности, компоненты Xi, i = l, …, n, являются N (Q, qu) -распре- qu) -распределенными ел. в. Ноказательство. Не ограничивая общности, положим Yfc = = (* ¦ Хк). Xn = UnB, В = [Ь \ Ь’п \, bi = (bu bnl), 7 = 1, -, «, E) и Un — Nn (On, / „) -распределенный вектор. векторов bi, …, bfc к ортонормированной системе С |, …, с „таким образом следовательно, что Ьу = Ь /, с, + … + Л // с /, ХцФ0, / = 1, …, л. F)

Если \ „= (Х \, …, Х„) имеет долю Wn @ n, Qn) с невырожденной матрицей Qn = \ qu, i, j = l, …, п] uYfc = (Xfl, Х, — „…, ХфЛ Людмила Фирмаль

Cатрица C = [c’i с ‘„] является ортогональной, а потому век- вектор Zn = UnC G) имеет выделение Nn @ n, In). Из E), F) и G) получить х, = и „ь; = и„ (х / гсг + … Uncj = XllZ1 + … + K, iZl, / = 1,2, …, л. (8) Индекс соотношения (8) значениями от 1 до k, получить, что вектор \ к = (Хи …, Хк) получен невырожденным линейным преобразованием из вектора (Zu …, Zk), имеющего iVfc @ *. /) — распределение, и, следовательно, Yft-нормальный вектор, очевидно, таковы, как это утверждается в лемме. Следствие. Пусть В = [Ьц, t = 1, …, n, / = 1 м] -nXm- матрнца ранга m, m <n, Qm = B’B, Un — N @ n, / ^ -распределенный вектор. имеет m-мерное нормальное распределение Wm (am, Qm) с невы- невырожденной матрицей ковариаций Qm.

Действительно, достаточно дополнить матрицу воспользоваться леммой 3. 4. Пусть вектор Х = (Хи …. Хп) имеет невырожденные невырожденное нормальное распределение, Y = (Xjt, …. X (m), Z = (Xtm + lt … • Си t), ede (j’i, / о. •••. ‘«) -определенная перестановка из чисел 103 A, 2 п). Если со \ г (Х; к, Xt ^^ O, k = l m; / = m-f 1, …, n, то очевидно Y н Z независимы. Воказательство. Вектор (Y, Z), полученный из нормального вектором X перестановкой координат, очевидно, нормален. коварнаций (Y, Z) имеет по условию вид \ Rv Om.n-m] Y.Z = | [На — м, м Rz J где 0, -, у вас имеется / Х / ‘-матрнцу, целиком состоящую из нулей. В таком случае (V’Z) ~ о R-1 {.На-м.м * Z J и Y, Z). нормальных плотностей: Nm @ m, RY) и JVn _ ,,, (On_m, Rz), что и до- доказывает утверждение.

Смотрите также:

• Примеры решения задач по статистике

Обобщенная линейная модель для семейства сдвига-масштаба	Случайные векторы с вырожденной матрицей ковариаций
Симметричное распределение	Вырожденное нормальное распределение

Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.