Оглавление:





Неустановившееся вязкое течение
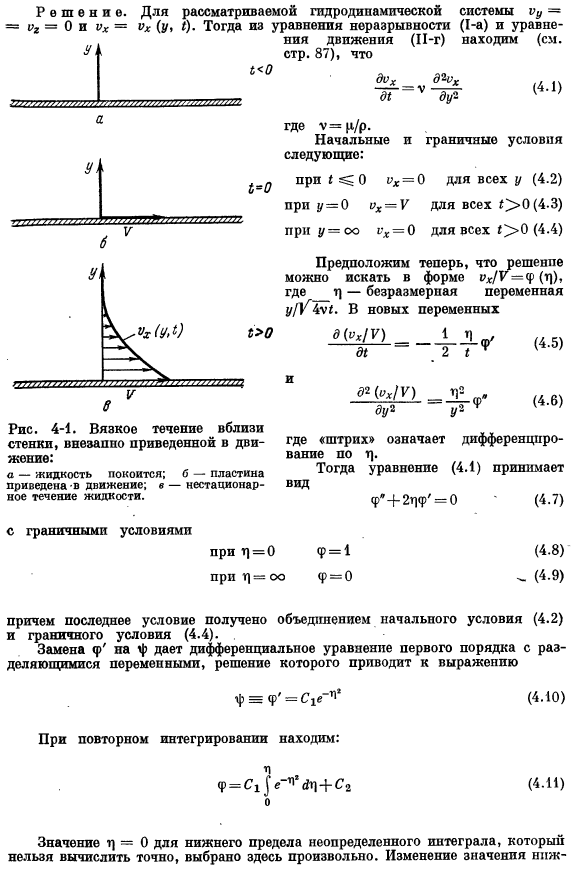
- Изучение всех типов переходных процессов приобретает все большее значение в связи с актуальным интересом к задачам, связанным с пусковым периодом и контролем. Уравнения, приведенные в главе 3, служат основой для описания нестационарных течений. Вот 2 примера, которые показывают, как такая проблема может быть сформулирована и решена*. Сначала рассмотрим поток неограниченного количества жидкости возле стенки, которая вдруг начала двигаться. В этой задаче показано применение метода подстановки переменных. Это позволяет свести дифференциальное уравнение в частных производных к 1 обыкновенному дифференциальному уравнению.
Это решение возможно только в том случае, если вы можете объединить 2 граничных условия в 1.It следует отметить, что такие гидродинамические системы никогда не достигают пределов стационарного состояния. Во 2-м примере анализируется переходный режим течения вязкой жидкости в трубе. Эта задача решается методом разделения переменных. Это позволяет свести дифференциальное уравнение в частных производных к 2 обыкновенным дифференциальным уравнениям. Тем не менее, этот тип течения имеет предельный профиль скорости, когда время устремляется к бесконечности, То есть когда гидродинамическая система достигает стационарного состояния.
Уравнение может быть сделано безразмерным путем введения величин со штрихами: (9-24) (9-25) Граничные условия должны задать скорость, давление и температуру на границах. Людмила Фирмаль
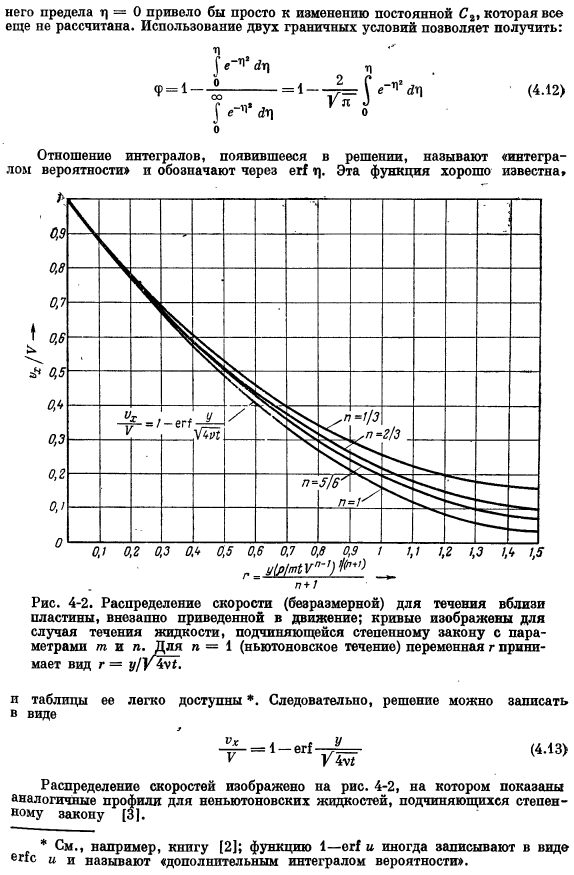
Если его предел μ= 0, то происходит изменение константы С, которая еще не вычислена. Используя 2 граничных условия, можно получить: Цифры 4-2.Распределение скорости потока вблизи пластины внезапно начало двигаться (безразмерно).Показана кривая для жидкости по степенному закону параметра typ. если n = 1 (поток Ньютона), то переменная r принимает вид r = y / Um. Эта таблица легко доступна*.Таким образом, вы можете написать решение (4.13)) Скорость и изображение Вероятность.* 0 и VR = ви(т, е. серийный(1-6) и г Начальные и граничные условия следующие: для r = H»r = 0 За мной!
- Безразмерные переменные: (РО-Р) Яг / 4-м Я (4.14)) (4-15) (4-16) (4-17) (4.18)) (4.19)) (4-20). Найти безразмерную скорость путем деления на максимальное значение с I = oo. Если умножить все члены безразмерной переменной, то получится: (4.21) (4.22) Решение предельной функции φ » (E, 4). к уравнению (4.21) Другими словами, общее решение делится на случай стационарного течения pco(5)и случай перехода 1 для нахождения стационарного решения, где DP / dm = 0 подставляется. (4.23) Если 5 = 1, то граничное условие p = 0 (4.24) Сорость пения. Замена введения следующей функции приобретения φ на производную Мы будем искать решение здесь FD8.
Замените указанное решение б =c₁₁/ о (А5)+ с * У0 («6) Где C₀₁₁₁₁cx и ХГ являются 1-й и 2-й и 7th₀, соответственно. Используйте начальные и граничные условия. Первое граничное условие. Поскольку это конечная величина, она конечна. Во время Интеграла Cr ₀ ₀ (A5) -> так как он есть, он должен быть установлен в ноль. 2-е граничное условие. _0 at должно исчезнуть, даже если ₍5 = 1.Это когда 7₀ (a) равно нулю. Но график функции 7₀(а) Начальное состояние. Я знаю, но b фу = Т = 0, суперпозиция РН5.Т)= 2л » / о («П5) (4.35 )) (4.36)) Чтобы определить коэффициент Bn, умножьте обе стороны последнего соотношения на 7₀ (Хя5) 6Å Å) и интегрируйте их от 0 до 1.
Дополнительный член и(др1дх) появляется в уравнении энергии, свидетельствуя о том, что в сжимаемом потоке температура изменяется, когда сжатие или расширение вызвано изменением давления. Людмила Фирмаль
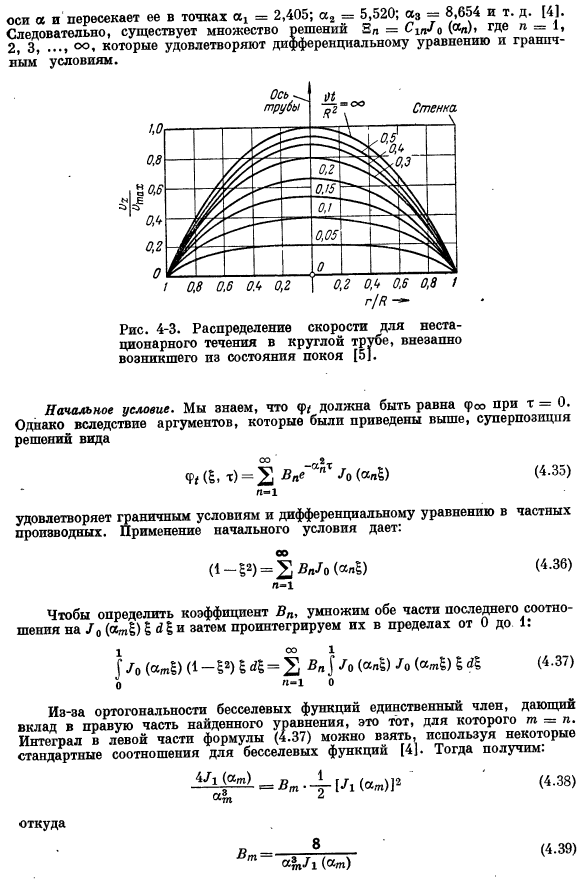
Из-за ортогональности функции. Бесселя единственным членом, который вносит вклад в правую часть найденного уравнения, является член M=.Интеграл выражения (4.37) может быть получен с использованием нескольких стандартных функций Бесселя[4].Тогда мы получаем: («Т) П (4.38) Откуда (4.39) Шовное представление безразмерного распределения скоростей (4.40 утра )) На рисунке показан профиль скорости, рассчитанный по формуле (4.40). 4-3.Затем максимальная скорость (по оси трубы) В пределах 10% от соответствующего значения Юя Стационарное течение Это был отличный опыт.
Смотрите также:

