Неравенство о сумме двух взаимно обратных чисел
Обратным к числу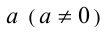 
называется, по определению, число 1 /а.
Теорема (неравенство о сумме двух взаимно обратных чисел).
1) Если а > 0, то справедливо неравенство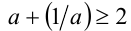 
, причём неравенство обращается в равенство только при а = 1.
2) Если а < 0 , то справедливо неравенство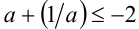 
, причём неравенство обращается в равенство только при а = — 1.
Доказательство. 1) Пусть а > 0 . Умножив неравенство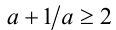 
на а (с сохранением знака), получим равносильное неравенство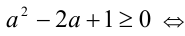 
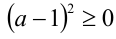, которое, очевидно, верно. Причём последнее неравенство, а, значит, и доказываемое обращаются в равенство тогда и только тогда, когда а = 1 .
2) Пусть а < 0 . Тогда неравенство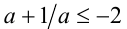 
равносильно после умножения на а (с учётом знака) очевидному неравенству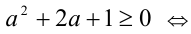 
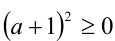причём последнее неравенство, а, следовательно, и доказываемое, обращаются в равенства тогда и только тогда, когда а = — 1.
Следствие 1. Для любого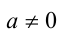 
справедливо неравенство 
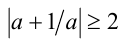, причём равенство достигается только при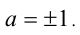 
Следствие 2. Если а и b — два числа одного знака, т.е. ab > 0, то спра-ведливо неравенство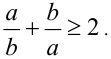 
Пример. Доказать, что для положительных чисел а ,b и c справедливо неравенство (Минковского)
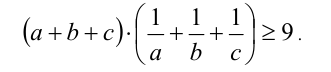
Доказательство. Раскроем скобки и сгруппируем вместе образующиеся при этом пары взаимно обратных чисел:
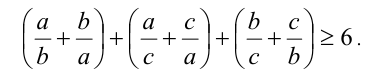
Так как каждое из трёх выражений в скобках, очевидно, не меньше 2, то неравенство доказано.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
