Неравенство между средним арифметическим и средним квадратичным
Теорема. Для любых неотрицательных действительных чисел 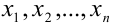
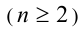 справедливо неравенство
справедливо неравенство
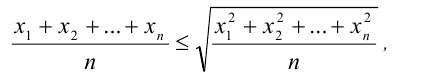
которое обращается в равенство, только если 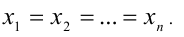
Доказательство. Согласно неравенству Коши-Буняковского имеем
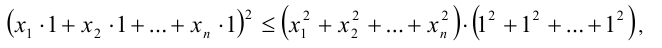
откуда после деления на 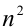 и извлечения квадратного корня из обеих частей неравенства получаем искомое неравенство. Равенство имеет место тогда и только тогда, когда
и извлечения квадратного корня из обеих частей неравенства получаем искомое неравенство. Равенство имеет место тогда и только тогда, когда 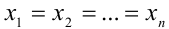 .
.
Пример. Доказать, что для неотрицательных чисел а,b,c имеет место неравенство
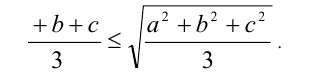
Доказательство. Для начала возведём доказываемое неравенство в квадрат
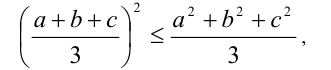
затем умножим обе его части на 9:
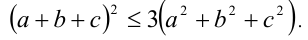
Раскроем теперь квадрат в левой части и перенесём после этого все слагаемые направо. Выделяя затем три полных квадрата, приходим к очевидному неравенству (эквивалентному доказываемому)
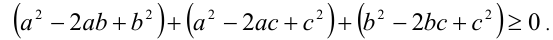
Таким образом, неравенство доказано.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

