Неравенство Коши-Буняковского
Буняковский Виктор Яковлевич (1804-1889) — русский математик, академик Петербургской АН. Математическое образование получил в Париже. Преподавал в Петербургском университете. Работал в области теории чисел и теории вероятностей. В математическом анализе занимался теорией неравенств.
Теорема (неравенство Коши-Буняковского). Для любых действительных чисел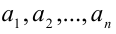 
и 
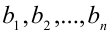справедливо неравенство
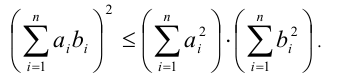
Доказательство. Воспользуемся для доказательства очевидным алгебраическим неравенством:
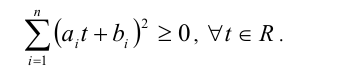
Раскрыв квадрат суммы, преобразуем это неравенство к виду
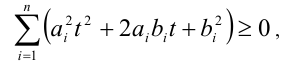
и разобьём левую часть на сумму трёх слагаемых
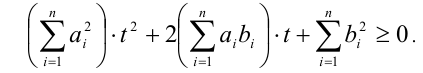
Обозначив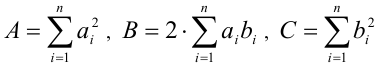 
, получим, что квадратное неравенство 
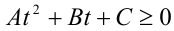должно выполняться сразу при всех действительных значениях переменной t. Исключая тривиальный случай, когда все числа 
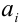одновременно обращаются в нуль, имеем А > 0 и, следовательно, неравенство верно при всех t тогда и только тогда, когда дискриминант квадратного трехчлена 
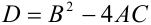неположителен, т.е.
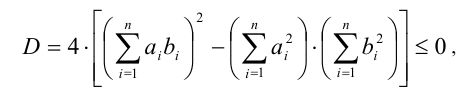
откуда и вытекает необходимое неравенство.
Замечание. Неравенство Коши-Буняковского обращается в равенство тогда и только тогда, когда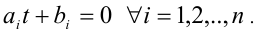 
Если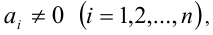 
то условие обращения неравенства в равенство можно записать в виде условия пропорциональности чисел 
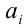и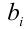 
:
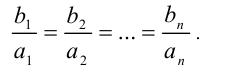
Некоторые авторы применяют эту форму записи условия и в общем случае, когда отдельные (или даже все сразу) из чисел 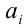могут обращаться в нуль. При этом дополнительно оговаривается, что если некоторое 
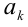равно нулю, то и соответствующее
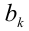также должно обращаться в нуль.
Пример. Пусть а + b +c =1 . Доказать справедливость неравенства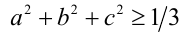 
для произвольных действительных чисел а,b,c .
Доказательство. Воспользуемся неравенством Коши-Буняковского
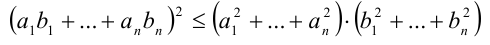
при n = 3, полагая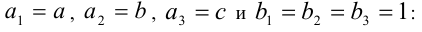 
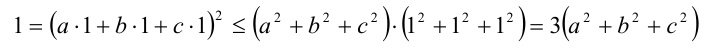
После деления обеих частей последнего неравенства на 3 получаем исходное неравенство доказанным.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
