Оглавление:

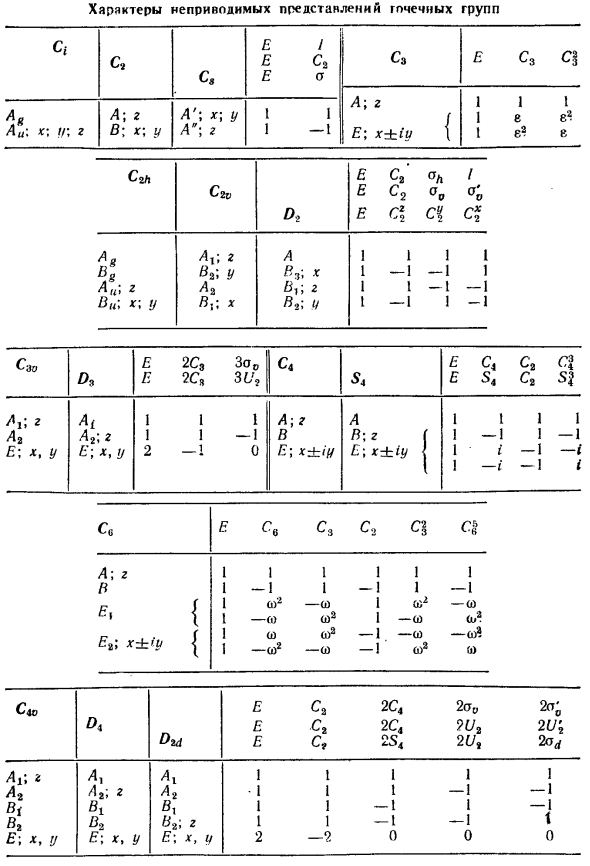




Неприводимые представления точечных групп
- Неприводимое представление облака точек Теперь посмотрим на неприводимое конкретное определение Представление группы точек. Большинство молекул Имеет только вторую, третью, четвертую и четвертую оси симметрии. 6 первичными. Поэтому группы не рассматриваются Икосаэдр Y, Y h; группа C n, C nh, C nv, D n, D nh.
- Поиск только по значениям n = 1, 2, 3, 4, 6 и группе S 2t D для n = 1, 2, 3. Таблица показывает характер представления этих групп. С 7. Морфологические группы имеют одинаковое представление и лидерство Объедините их в один стол. Номер перед символом товара Первая строка группы показывает количество элементов соответственно Класс (см. §93).
Первый столбец Традиционная запись для выражений. Людмила Фирмаль
Одномерный пред Настройки показаны буквой A, B, 2D-буквой E, И 3D-F (обозначение E для 2D без привода) Не путайте с обозначением Е для унификации выражения Личный элемент группы! ) 1). Функции на основе выражений A симметрична, а функция B асимметрична относительно Вращение вокруг n-й главной оси. функция Различная симметрия относительно отражения.
Количество ударов (1 или 2) и индекс г и Указывает симметрию относительно инверсии. Наряду с Обозначения выражения по буквам x, y, z Координаты преобразуются в представления. 2 оси в любом месте Выбирается вдоль главной оси симметрии. Буквы e и u обозначают следующее: e = e2 ™ / 3, w = e2 ™ / 6 = -w 4, + +2 2 = -1, 2 2-0J = -1.
Самое простое определение неприводимого выражения Для путешествующей группы (группа C n, Sn). Циклическая группа Как и абелева группа, она имеет только одномерное представление Забытый лаз. G является элементом генерации группы (т.е. элементом Поднимайте это постоянно, чтобы получить все Группа полицейских). Gg = E (g — групповой порядок), поэтому г).
Два комплексных сопряженных одномерных пред Формулировка показана в виде одного двумерного и находится в §96. Когда оператор G работает на базисных функциях Последнее можно умножить только на ^ 1. Иными словами, 1) Gip = e2wik / gi>, k = 1,2. , , Г. Группа C 2h (и того же типа C 2v и D 2) является абелевой, поэтому Неприводимые выражения все одномерные и имеют Бактерии могут быть равны только ± 1 (каждый квадрат Элемент E).
Далее рассмотрим группу C ^ v. Сравнить с группой C * 3 Здесь добавлено отражение av в вертикальной плоскости (Все относится к одному классу). Инвариантные функции Относительное значение для вращения вокруг оси (базисная функция Группа A Группа C s), симметричная или антисимметричная Метрика об отражении crv. Функция умная Это потому, что С3 вращается на £ и е2 (базисная функция.
Однако когда отражается сопряженное выражение E), 2) друг друга. Исходя из этих аргументов, группа C% v (И X? S изоморфизм) имеет два одномерных и один два измерения Неприводимое представление с символами, обозначенными г) Для точечной группы C n, как функция от φ, например: Возьмем функцию φ = exp1p (k = 1, 2, …, n). Где (р — угол поворота вокруг оси. Считая с определенного направления, 2) Эти функции можно использовать, например, в виде φ1 = e1p, φ2 = e-1p. в
- Отражение на вертикальной плоскости (смена знака. Табл. Представление, итого I 2 + I 2 + + 22 = 6, т. Е. Равен групповому порядку. Аналогичные рассуждения были найдены для предыдущего письма Представление других групп того же типа (C ^, C qv). Группа Т из группы D 2 = V Рот вокруг 4-й оси наклона. испуг Инвариант для преобразования группы V (Основное выражение A), вы можете умножить, повернув C3 1, £ или £ 2.
Основные функции трех одномерных представлений Слияние B ±, ^ 2, группа V при повороте третьей оси Передайте друг другу по порядку (как вы можете видеть, если вы берете Для этих функций сами координаты x, y, z). так Следовательно, три одномерных и один трехмерный Приемлемое представление (1 2 + 12 + 12 + 32 = 12). Наконец, рассмотрим группы изоморфизмов 0 и T ^.
Организация pa Td получается путем добавления отражения от группы T. Людмила Фирмаль
Самолет, который проходит через две оси Этого заказа. Базисная функция единичного представления A Группа Т является симметричной или антисимметричной Связанные с этими размышлениями (все связанные с одним Class), предоставляет два одномерных представления группы T &. Функция умножается на £ или £ 2 при вращении вокруг оси.
Третий порядок (основные комплексные конъюгаты) Группа E), при отражении на проходящем самолете Если вы обрежете эту ось и войдете друг в друга, вы увидите одну вещь Двумерное представление. Наконец, из трех базисных функций представления группы F Только T преобразуется, чтобы отразить себя (и Может остаться без изменений или знак может измениться) Передайте друг другу.
Таким образом, вы получаете только два шанса Число, одно двумерное и два трехмерных представления 1). Для других интересных мест, Тогда их идеи могут быть получены непосредственно от Если вы заметите, что эти группы являются прямыми, вы будете уволены.
В зависимости от группы продуктов, уже рассмотренных группой C { (Или С 3). просто Csh = C ^ x C s, D 2h = D 2 x C i, D ^ d = D ^ x C i, 0 ^ = 0 xCj, C4h = C4: x C i, D ^ h = D ^ x C i, DQh = D Q x C i, C ^ n-C ^ x C g, S q = C ^ x C i, T n = T x C g г) многомерное неприводимое представление (4-й И 5-е) относятся к группе икосаэдров.
Каждая из этих прямых работ удваивается Неприводимое представление, чем исходная группа, и Один из них симметричный (обозначен индексом g) Половина асимметрична (индекс i) Версия. Символы в этих представлениях являются производными от символов Представление исходной группы путем умножения на ± 1 (каждый По правилам (94.24)). Итак, для группы D ^ d мы получаем: Установка:
Смотрите также:
| Точечные группы | Неприводимые представления и классификация термов |
| Представления групп | Правила отбора для матричных элементов |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

