Оглавление:
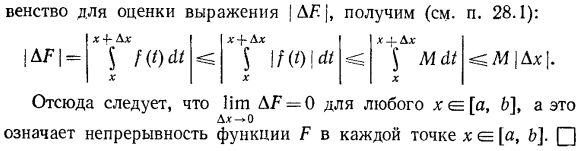

Непрерывность интеграла по верхнему пределу.
Непрерывность интеграла по верхнему пределу. Предположим, что функция f (x) интегрируема с интервалом [a, b.It затем может быть интегрирован в любой сегмент[a, x].Где ^ х ^ б、 Икс То есть для xe [a, b] Интеграл имеет смысл Но… Подумайте о возможностях Икс Е (*)= $ /(1) Д1. (29.1) Но…
Эта функция определяется интервалом [a, b] и называется интегралом с переменной верхней границей. Установите базовое свойство. Людмила Фирмаль
- Теорема 1.Если функция / интегрируема на интервале[a, b], то функция (29.1) непрерывна на этом интервале. Доказательство. Из Формулы (29.1)、 ХД-а * П(х + ДХ)= ^ /(0 *Й= Но… * = $ /(0Л + * + $ л * /(0 и = п(х)+ икс X + LA + $ /(0 ^. икс.
- Таким образом (рис. 109) Де = е(х + ДХ) / 7(х)= *+д * * = 5(29,2) Икс То есть для каждого 1E [a, b]существует постоянная M 0, которая равна| / (x) / = ecM. To применить это 468§ 29.
Функция f интегрируется на интервале[a, b], поэтому она ограничена этим интервалом. Людмила Фирмаль
- Постоянный Интеграл с переменным верхним пределом | Д ^ | = х \ ой 5 МП Икс Ми Ай 1 X + A * $ 1 /(0!Н х + ДХ 5 Н1) С Чтобы оценить выражение testiment / DR|, get (см.§ 28.1). То есть, АРАРАР = = = 0 для любого X E [A, B], который равен ДХ » 0 Означает непрерывность функции P в каждой точке x e [a, b]. (3)
Смотрите также:

