Непрерывность сложной функции
Теорема 4.6. Пусть функция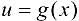 
непрерывна в точке 
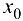, функция 
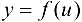непрерывна в точке 
, тогда сложная функция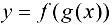 
непрерывна в точке .
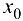Доказательство.
В силу непрерывности функции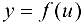 
в точке 
: 
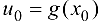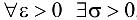, такое, что для 
.
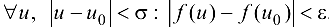В силу непрерывности функции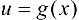 
в точке 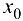для найденного 
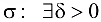, такое, что для 
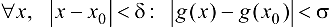, т. е. 
—
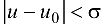Таким образом,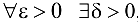 
, такое, что для 
: 
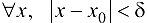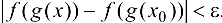
Следовательно, функция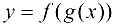 
непрерывна в точке . ■
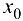Следствие 4.1. Знак предела и знак непрерывной функции можно менять местами, т. е.
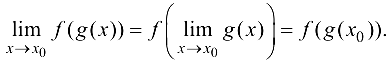
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
