Непрерывность функции в точке. Классификация точек разрыва
Функция 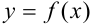 , определенная на интервале
, определенная на интервале 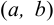 , называется непрерывной в точке
, называется непрерывной в точке 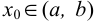 , если
, если 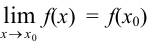 , т. е. предел функции равен ее значению при предельном значении аргумента. Для непрерывности функции в точке
, т. е. предел функции равен ее значению при предельном значении аргумента. Для непрерывности функции в точке 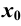 требуется выполнение трех условий:
требуется выполнение трех условий:
- Точка должна принадлежать области определения функции. Функция должна быть определена и в некоторой окрестности точки
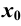 .
. - Функция
 должна иметь конечный предел в точке
должна иметь конечный предел в точке 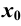 , т. е.
, т. е. 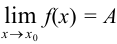 .
. - Этот предел
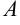 должен быть равен значению функции в этой точке, т. е.
должен быть равен значению функции в этой точке, т. е. 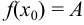 .
.
Если соотношение 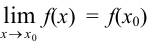 не имеет смысла, то функция называется разрывной в точке
не имеет смысла, то функция называется разрывной в точке 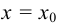 , а сама точка
, а сама точка 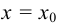 называется точкой разрыва функции
называется точкой разрыва функции  .
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

