Оглавление:
Непрерывность функции в точке
Пусть функция  определена в точке
определена в точке  и в некоторой окрестности этой точки. Функция
и в некоторой окрестности этой точки. Функция  называется непрерывной в точке
называется непрерывной в точке  , если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.
, если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.

Равенство (19.1) означает выполнение трех условий:
1) функция  определена в точке
определена в точке  и в ее окрестности;
и в ее окрестности;
2) функция  имеет предел при
имеет предел при  ;
;
3) предел функции в точке  равен значению функции в этой точке, т. е. выполняется равенство (19.1).
равен значению функции в этой точке, т. е. выполняется равенство (19.1).
Так как 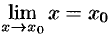 , то равенство (19.1) можно записать в виде
, то равенство (19.1) можно записать в виде
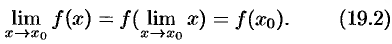
Это означает, что при нахождении предела непрерывной функции  можно перейти к пределу под знаком функции, то есть в функции
можно перейти к пределу под знаком функции, то есть в функции  вместо аргумента
вместо аргумента  подставить его предельное значение
подставить его предельное значение  .
.
Например, 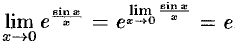 . В первом равенстве функция и предел поменялись местами (см. (19.2)) в силу непрерывности функции
. В первом равенстве функция и предел поменялись местами (см. (19.2)) в силу непрерывности функции 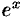 .
.
Пример №19.1.
Вычислить 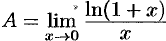 .
.
Решение:
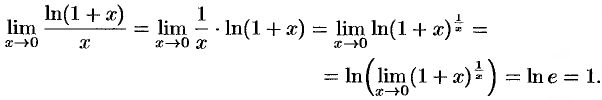
Отметим, что 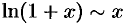 при
при 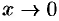 .
.
Можно дать еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции.
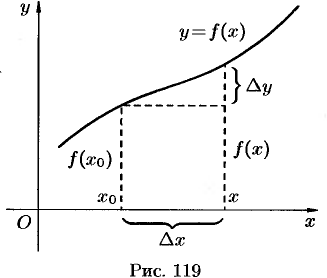
Пусть функция  определена в некотором интервале
определена в некотором интервале 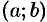 . Возьмем произвольную точку
. Возьмем произвольную точку 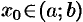 . Для любого
. Для любого 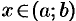 разность
разность 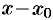 называется приращением аргумента
называется приращением аргумента  в точке
в точке  и обозначается
и обозначается 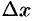 : («дельта
: («дельта  »)
») 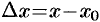 . Отсюда
. Отсюда 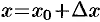 .
.
Разность соответствующих значений функций 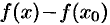 называется приращением функции
называется приращением функции  в точке
в точке  и обозначается
и обозначается 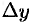 (или
(или  или
или 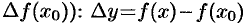 или
или 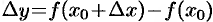 (см. рис. 119).
(см. рис. 119).
Очевидно, приращения 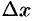 и
и 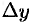 могут быть как положительными
могут быть как положительными
так и отрицательными числами.
Запишем равенство (19.1) в новых обозначениях. Так как условия  и
и 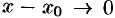 одинаковы, то равенство (19.1) принимает вид
одинаковы, то равенство (19.1) принимает вид 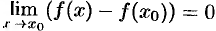 или
или

Полученное равенство (19.3) является еще одним определением непрерывности функции в точке: функция  называется непрерывной в точке
называется непрерывной в точке  , если она определена в точке
, если она определена в точке  и ее окрестности и выполняется равенство (19.3), т. е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
и ее окрестности и выполняется равенство (19.3), т. е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Исследуя непрерывность функции в точке, применяют либо первое (равенство (19.1)), либо второе (равенство (19.3)) определение.
Дополнительный пример №19.2.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Предельный переход в неравенствах |
| Предел монотонной ограниченной последовательности |
| Непрерывность функции в интервале и на отрезке |
| Точки разрыва функции и их классификация |

