Оглавление:
Понятие о непрерывности функции в точке является одним из основных понятий математического анализа. Существует несколько тождественных определений о функции, непрерывной в точке. В различных случаях целесообразно использование разных определений непрерывности.
Определение 1 (базовое). Функция 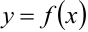 называется непрерывной в точке
называется непрерывной в точке 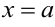 , если она определена в этой точке и её окрестности, и если существует конечный предел при
, если она определена в этой точке и её окрестности, и если существует конечный предел при 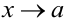 , равный значению функции в этой точке:
, равный значению функции в этой точке: 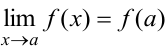 .
.
Определение 2. Функция 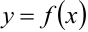 называется непрерывной в точке
называется непрерывной в точке 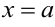 , если: 1) функция определена в этой точке и её окрестности; 2) существуют конечные односторонние пределы при
, если: 1) функция определена в этой точке и её окрестности; 2) существуют конечные односторонние пределы при 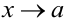 , равные между собой; 3) пределы равны значению функции в этой точке, т.е.
, равные между собой; 3) пределы равны значению функции в этой точке, т.е.
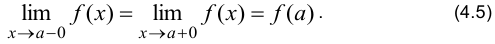
Данное определение удобно использовать при исследовании функций на непрерывность.
Функция непрерывна в интервале (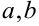 ), если она непрерывна в каждой точке этого интервала.
), если она непрерывна в каждой точке этого интервала.
Функция непрерывна на отрезке 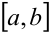 , если она непрерывна в каждой точке интервала (
, если она непрерывна в каждой точке интервала (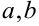 ) и если
) и если 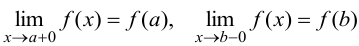 .
.
Если не выполняется одно из условий непрерывности функции в точке, то эта точка является точкой разрыва. В зависимости от того, какие значения принимают односторонние пределы в точке разрыва, различают точки разрыва 1-го и 2-го рода. Точки разрыва 1-го рода: точки устранимого разрыва (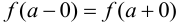 ); точки скачка, когда конечные односторонние пределы не равны между собой. В точках разрыва 2-го рода, односторонние пределы не существуют или равны бесконечности.
); точки скачка, когда конечные односторонние пределы не равны между собой. В точках разрыва 2-го рода, односторонние пределы не существуют или равны бесконечности.
Пример выполнения задания
Пример:
Задана функция 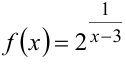 . Найти точку разрыва функции и исследовать её характер.
. Найти точку разрыва функции и исследовать её характер.
Решение:
Заданная функция определена при всех значениях аргумента, кроме 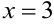 . Поэтому
. Поэтому 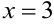 — точка разрыва функции. Определяем односторонние пределы в точке разрыва.
— точка разрыва функции. Определяем односторонние пределы в точке разрыва.
Пусть 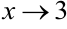 слева, т.е. выполняется неравенство
слева, т.е. выполняется неравенство 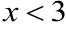 . Тогда разность
. Тогда разность 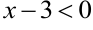 — отрицательная бесконечно малая величина. Выражение
— отрицательная бесконечно малая величина. Выражение 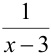 в этом случае — бесконечно большая отрицательная величина. Левосторонний предел:
в этом случае — бесконечно большая отрицательная величина. Левосторонний предел: 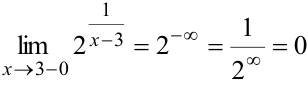 .
.
Пусть теперь 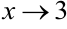 справа, т.е. выполняется неравенство
справа, т.е. выполняется неравенство 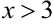 . Тогда разность
. Тогда разность 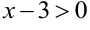 — положительная бесконечно малая величина. Выражение
— положительная бесконечно малая величина. Выражение 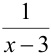 в этом случае — бесконечно большая положительная величина. Правосторонний предел
в этом случае — бесконечно большая положительная величина. Правосторонний предел 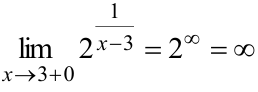 .
.
Так как один из односторонних пределов равен бесконечности, точка 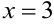 — точка разрыва второго рода.
— точка разрыва второго рода.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:

