Непрерывность функции двух переменных
Функция 
(или 
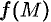) называется непрерывной в точке 
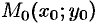, если она:
а) определена в этой точке и некоторой ее окрестности,
б) имеет предел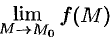 
,
в) этот предел равен значению функции 
в гонке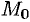 
, т. е.
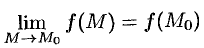или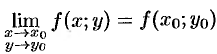 
.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва могут образовывать целые линии разрыва. Так, функция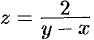 
имеет линию разрыва 
.
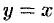Можно дать другое, равносильное приведенному выше, определение непрерывности функции в точке. Обозначим 
, 
, 
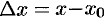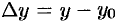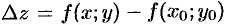. Величины 
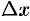и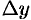 
называются приращениями аргументов 
и 
, а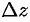 
— полным приращением функции 
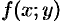в точке .
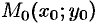Функция называется непрерывной в точке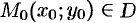 
, если выполняется равенство 
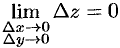, т. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов и стремятся к нулю.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям — подобные теоремы имели место для функций одной переменной (см. п. 19.4).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Приближенное вычисление определенного интеграла |
| Предел функции двух переменных |
| Свойства функций, непрерывных в ограниченной замкнутой области |
| Частные производные первого порядка |
