Понятие непрерывности функции двух действительных переменных в точности такое же, что и для случая функции одной переменной.
Пусть функция 
определена в точке 
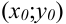и некоторой ее окрестности. Функция называется непрерывной в точке 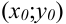, если существует предел функции в этой точке, и он равен значению функции в этой точке, т.е.
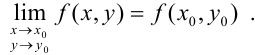
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. График непрерывной функции двух переменных представляет собой поверхность без разрывов, «проколов» и других особенностей.
Для непрерывных функций двух действительных переменных справедливы основные теоремы, выражающие «арифметические» свойства непрерывных функций, непрерывность сложной функции. Их формулировки дословно повторяют одномерный случай и поэтому нс приводятся (лекция 10 части 1).
Рассмотрим без доказательства теорему о свойствах функций двух действительных переменных, непрерывных в ограниченной замкнутой области, являющихся аналогом свойств непрерывных на отрезке функций одной переменной.
Теорема 1. Если функция непрерывна в ограниченной замкнутой области, то она в этой области:
- ограничена, т.е. существует такое число
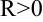, что для всех точек 
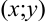в этой области выполняется неравенство 
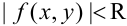; - имеет точки, в которых принимает наименьшее m и наибольшее
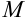значения; - принимает хотя бы в одной точке области любое численное значение, заключенное между
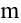и .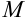
Точки, в которых нарушается непрерывность функции двух действительных переменных, называются точками разрыва этой функции.
У функции двух переменных множество точек разрыва бывает самым разнообразным. Например, функция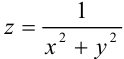 
имеет единственную точку разрыва (0;0), а функция 
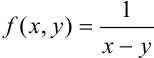разрывна на всей прямой 
.
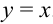Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
