Непрерывность элементарных и сложных функций

К непрерывным на области определения относятся все основные элементарные функции:

1. , где ;
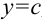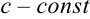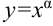2. , где 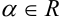— степенная функция;
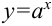3. , где 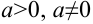— показательная функция;
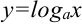4. , где 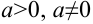— логарифмическая функция;
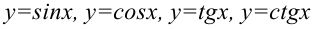5. — тригонометрические функции;
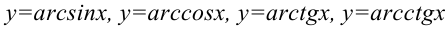6. — обратные тригонометрические функции.

Всякие функции, которые получаются из основных элементарных путем выполнения над ними конечного числа арифметических операций или составления сложных функций называются элементарными функциями.

Вее элементарные функции непрерывны на области определения.

Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.

Пример №10.2.

Найдите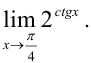

Решение:

Функция 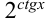непрерывна в точке 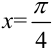, поэтому ее предел совпадает со значением функции в этой точке: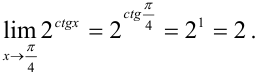

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Основные теоремы о непрерывных функциях.

Свойства функций, непрерывных на отрезке.

Точки разрыва, их классификация.

Понятие производной функции.