Оглавление:
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример №19.1.
Найдите 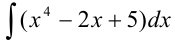 .
.
Решение:
Воспользуемся свойствами неопределенного интеграла: представим интеграл как сумму и разность соответствующих интегралов:
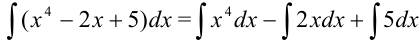 . Вынесем константы за знак интеграла:
. Вынесем константы за знак интеграла:
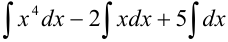 и воспользуемся табличными интегралами. Получим, что
и воспользуемся табличными интегралами. Получим, что
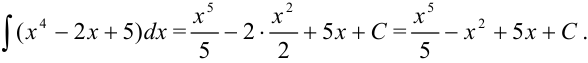
Пример №19.2.
Найдите 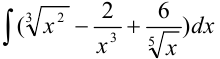 .
.
Решение:
Каждое слагаемое, стоящее под знаком интеграла, представим в виде степени с рациональным показателем. Для этого применим следующие свойства степени: 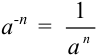 ;
; 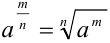 . Тогда
. Тогда 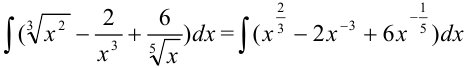 . Представим данный интеграл как сумму и разность интегралов, вынесем константы за знак интеграла:
. Представим данный интеграл как сумму и разность интегралов, вынесем константы за знак интеграла:
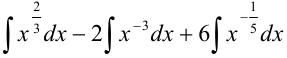 . Воспользовавшись табличным
. Воспользовавшись табличным
интегралом 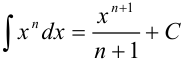 , получим:
, получим:
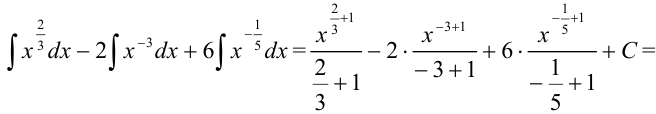
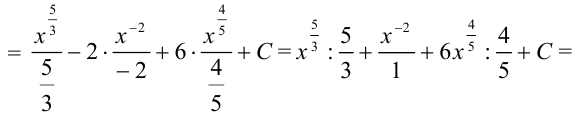
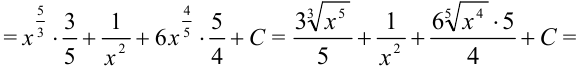
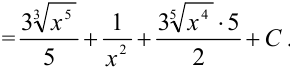
Пример №19.3.
Найдите 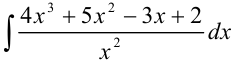 .
.
Решение:
Разделив почленно числитель на знаменатель, получим
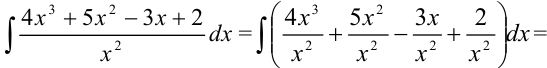
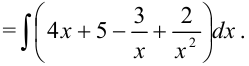
Представим данный интеграл как сумму и разность интегралов, вынесем константы за скобки:
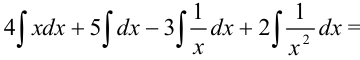
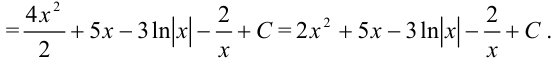
Пример №19.4.
Найти 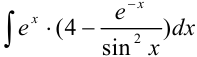 .
.
Решение:
Раскрывая скобки и применяя табличные интегралы, получим:
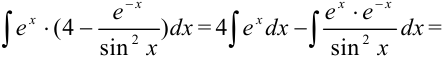
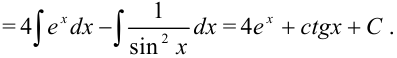
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Основные свойства неопределенного интеграла. |
| Таблица основных интегралов. |
| Интегралы от некоторых сложных функций. |
| Интегрирование методом замены переменной (методом подстановки). |

