Оглавление:
Неопределённые интегралы
Пусть функции 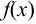 и
и 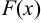 определены на множестве
определены на множестве 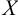 .
.
Функция 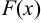 называется первообразной функцией для функции
называется первообразной функцией для функции 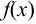 на множестве
на множестве 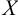 , если её производная
, если её производная  и дифференциал
и дифференциал 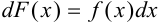 на
на 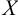 .
.
Теорема. Если 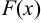 есть первообразная функция для
есть первообразная функция для 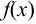 , то и функция
, то и функция 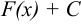 , где
, где  — произвольная постоянная, тоже будет первообразной для функции
— произвольная постоянная, тоже будет первообразной для функции 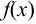 .
.
Доказательство.  .
.
Отсюда следует, что если функция 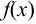 имеет хотя бы одну первообразную, то она будет иметь бесконечное множество первообразных функций.
имеет хотя бы одну первообразную, то она будет иметь бесконечное множество первообразных функций.
Совокупность всех первообразных функций 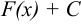 для функции
для функции 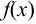 называется неопределённым интегралом функции
называется неопределённым интегралом функции 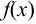 и обозначается
и обозначается 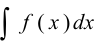 , т. е.
, т. е. 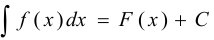 .
.
Свойства неопределённого интеграла
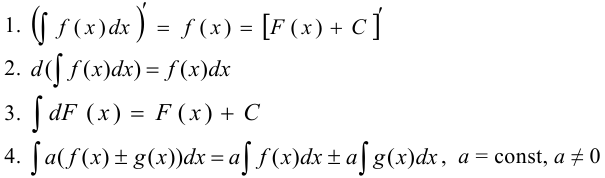
Таблица основных интегралов
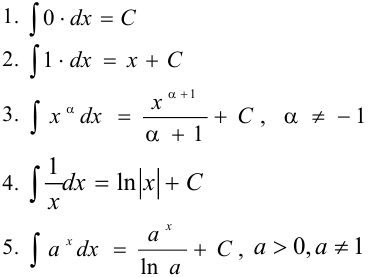
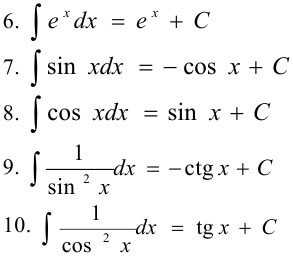
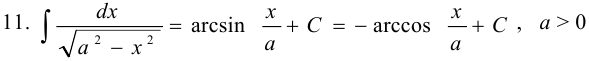
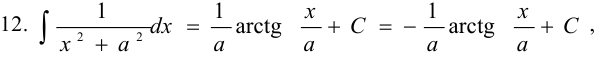
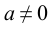
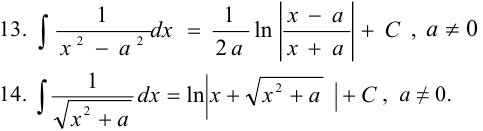
Задача №72.
Вычислить интеграл:
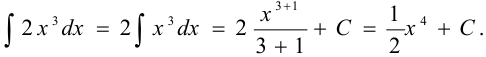
Проверка. Чтобы проверить правильность вычисления интеграла, надо от первообразной взять производную и получить подынтегральную функцию:
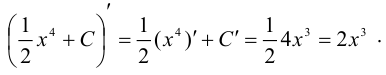
Задача №73.
Вычислить 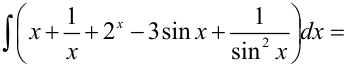
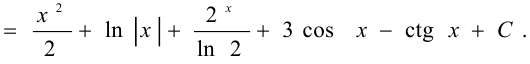
Задача №74.
Вычислить 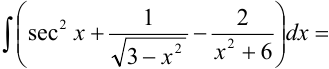
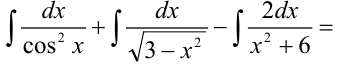
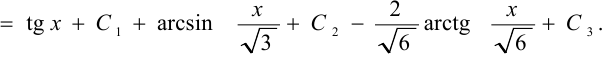
Задача №75.
Вычислить интеграл:
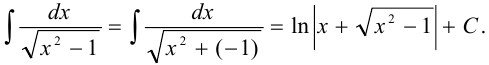
Задача №76.
Вычислить интеграл:
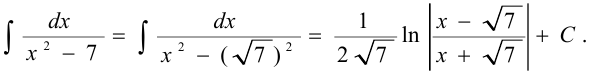
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

