Неоклассическая модель роста Р. Солоу
Неоклассические модели роста преодолевали ряд ограничений кейнсианских моделей и позволяли более точно описать особенности макроэкономических процессов.
Р. Солоу показал, что нестабильность динамического равновесия в кейнсианских моделях была следствием невзаимозаменяемости факторов производства. Вместо функции Леонтьева он использовал в своей модели производственную функцию Кобба-Дугласа, в которой труд и капитал являются субститутами.
Другими предпосылками анализа в модели Солоу являются: убывающая предельная производительность капитала, постоянная отдача от масштаба, постоянная норма выбытия, отсутствие инвестиционных лагов.
Взаимозаменяемость факторов (изменение капиталовооруженности) объясняется не только технологическими условиями, но и неоклассической предпосылкой о совершенной конкуренции на рынках факторов.
Необходимым условием равновесия экономической системы является равенство совокупного спроса и предложения. Предложение описывается производственной функцией с постоянной отдачей от масштаба:
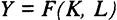
и для любого положительного 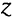 верно:
верно:
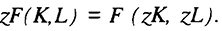
Тогда если
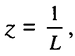
то
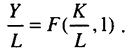
Обозначим 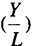 через
через 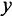 , а
, а 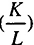 через
через 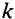 и перепишем исходную функцию в форме взаимосвязи между производительностью и фондовооруженностью (капиталовооруженностью):
и перепишем исходную функцию в форме взаимосвязи между производительностью и фондовооруженностью (капиталовооруженностью): 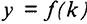 (см. рис. 11.1). Тангенс угла наклона данной производственной функции для каждого уровня
(см. рис. 11.1). Тангенс угла наклона данной производственной функции для каждого уровня 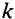 соответствует предельному продукту капитала (
соответствует предельному продукту капитала (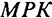 ), который убывает по мере роста фондовооруженности (
), который убывает по мере роста фондовооруженности (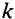 ).
).
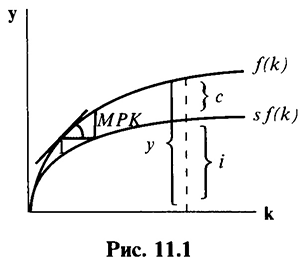
Совокупный спрос в модели Солоу определяется инвестициями и потреблением: 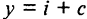 , где
, где 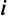 и
и 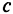 — инвестиции и потребление в расчете на одного занятого. Доход делится между потреблением и сбережениями в соответствии с нормой сбережения, так что потребление можно представить как
— инвестиции и потребление в расчете на одного занятого. Доход делится между потреблением и сбережениями в соответствии с нормой сбережения, так что потребление можно представить как 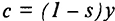 , где
, где 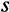 — норма сбережения (накопления), тогда
— норма сбережения (накопления), тогда 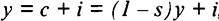 , откуда
, откуда 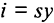 . В условиях равновесия инвестиции равны сбережениям и пропорциональны доходу.
. В условиях равновесия инвестиции равны сбережениям и пропорциональны доходу.
Условия равенства спроса и предложения могут быть представлены как 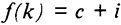 или
или 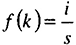 . Производственная функция определяет предложение на рынке товаров, а накопление капитала спрос на произведенный продукт.
. Производственная функция определяет предложение на рынке товаров, а накопление капитала спрос на произведенный продукт.
Динамика объема выпуска зависит от объема капитала (в нашем случае — капитала в расчете на одного занятого, или капиталовооруженности). Объем капитала меняется под воздействием инвестиций и выбытия: инвестиции увеличивают запас капитала, выбытие — уменьшает.
Инвестиции зависят от фондовооруженности и нормы накопления, что следует из условия равенства спроса и предложения в экономике:
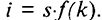
Норма накопления определяет деление продукта на инвестиции и потребление при любом значении 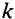 (рис. 11.1):
(рис. 11.1):
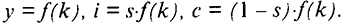
Амортизация учитывается следующим образом: если принять, что ежегодно вследствие износа капитала выбывает его фиксированная часть 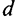 (норма выбытия), то величина выбытия будет пропорциональна объему капитала и равна
(норма выбытия), то величина выбытия будет пропорциональна объему капитала и равна 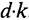 . На графике эта связь отражается прямой, выходящей из точки начала координат, с угловым коэффициентом
. На графике эта связь отражается прямой, выходящей из точки начала координат, с угловым коэффициентом 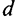 (рис. 11.2).
(рис. 11.2).
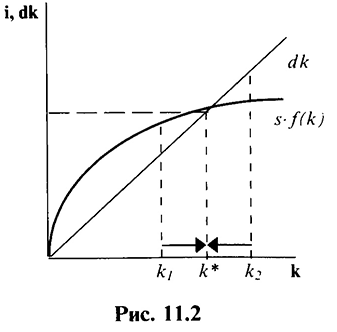
Влияние инвестиций и выбытия на динамику запасов капитала можно представить уравнением 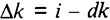 , или, используя равенство инвестиций и сбережений,
, или, используя равенство инвестиций и сбережений, 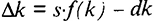 . Запас капитала
. Запас капитала 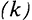 будет увеличиваться
будет увеличиваться 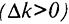 до уровня, при котором инвестиции будут равны величине выбытия, т.е.
до уровня, при котором инвестиции будут равны величине выбытия, т.е. 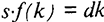 . После этого запас капитала на одного занятого (фондовооруженность) не будет меняться во времени, поскольку две действующие на него силы уравновесят друг друга
. После этого запас капитала на одного занятого (фондовооруженность) не будет меняться во времени, поскольку две действующие на него силы уравновесят друг друга 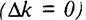 . Уровень запаса капитала, при котором инвестиции равны выбытию, называется равновесным (устойчивым) уровнем фондовооруженности труда и обозначается
. Уровень запаса капитала, при котором инвестиции равны выбытию, называется равновесным (устойчивым) уровнем фондовооруженности труда и обозначается 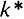 При достижении
При достижении 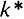 экономика находится в состоянии долгосрочного равновесия.
экономика находится в состоянии долгосрочного равновесия.
Равновесие является устойчивым, поскольку независимо от исходного значения 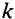 экономика будет стремиться к равновесному состоянию, т.е. к
экономика будет стремиться к равновесному состоянию, т.е. к 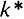 . Если начальное
. Если начальное 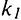 ниже
ниже 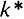 , то валовые инвестиции
, то валовые инвестиции 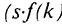 ) будут больше выбытия
) будут больше выбытия 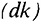 и запас капитала будет возрастать на величину чистых инвестиций. Если
и запас капитала будет возрастать на величину чистых инвестиций. Если 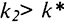 это означает, что инвестиции меньше, чем износ, а значит, запас капитала будет сокращаться, приближаясь к уровню
это означает, что инвестиции меньше, чем износ, а значит, запас капитала будет сокращаться, приближаясь к уровню 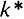 (см. рис. 11.2).
(см. рис. 11.2).
Норма накопления (сбережения) непосредственно влияет на устойчивый уровень фондовооруженности. Рост нормы сбережения с 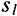 до
до 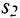 сдвигает кривую инвестиций вверх из положения
сдвигает кривую инвестиций вверх из положения 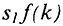 до
до 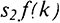 (см. рис. 11.3) характеризуется более высокими значениями фондовооруженности и производительности труда (выпуск на одного занятого, у).
(см. рис. 11.3) характеризуется более высокими значениями фондовооруженности и производительности труда (выпуск на одного занятого, у).
Модель Солоу показывает, что норма сбережения является важнейшим фактором, определяющим устойчивый уровень капиталовооруженности и, соответственно, уровень выпуска. Страны с более высокой нормой сбережения больше инвестируют и имеют более высокий уровень капиталовооруженности, что обеспечивает более высокий темп роста (см. табл. 11.1).
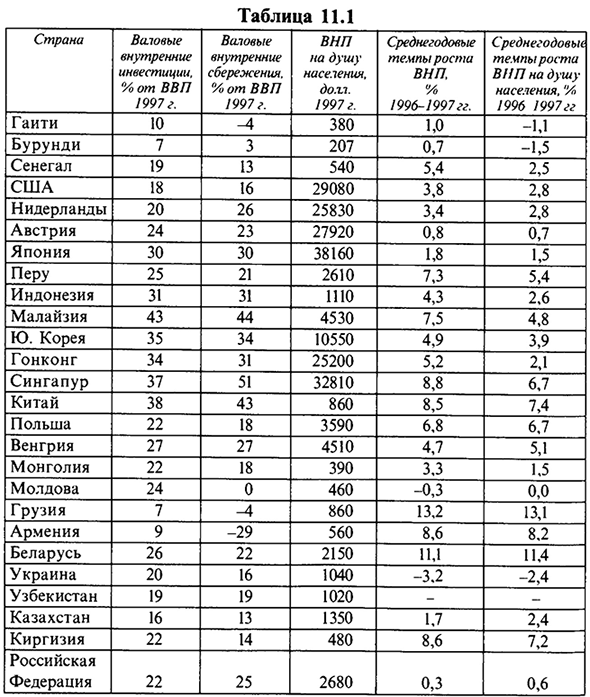
Таким образом, чем выше норма сбережения (накопления), тем более высокий уровень выпуска и запаса капитала может быть достигнут в состоянии устойчивого равновесия. Однако повышение нормы накопления ведет к ускорению экономического роста в краткосрочном периоде, до тех пор пока экономика не достигнет точки нового устойчивого равновесия.
Очевидно, что ни сам процесс накопления, ни увеличение нормы сбережения не могут объяснить механизм непрерывного роста выпуска в рассчете на душу населения в устойчивом состоянии. Они показывают лишь переход от одного состояния равновесия к другому.
Для дальнейшего развития модели Солоу поочередно снимаются две предпосылки: неизменность численности населения и его занятой части (их динамика предполагается одинаковой) и отсутствие технического прогресса.
Предположим, население растет с постоянным темпом 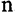 . Это новый фактор, влияющий вместе с инвестициями и выбытием на фондовооруженность. Теперь уравнение, показывающее изменение запаса капитала на одного работника, будет выглядеть как
. Это новый фактор, влияющий вместе с инвестициями и выбытием на фондовооруженность. Теперь уравнение, показывающее изменение запаса капитала на одного работника, будет выглядеть как
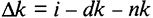
или
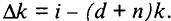
Рост населения аналогично выбытию снижает фондовооруженность, хотя и по-другому — не через уменьшение наличного запаса капитала, а путем распределения его между возросшим числом занятых. В данных условиях необходим такой объем инвестиций, который не только бы покрыл выбытие капитала, но и позволил бы обеспечить капиталом новых рабочих в прежнем объеме. Произведение 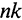 показывает, сколько требуется дополнительного капитала в расчете на одного занятого, чтобы капиталовооруженность новых рабочих была на том же уровне, что и старых.
показывает, сколько требуется дополнительного капитала в расчете на одного занятого, чтобы капиталовооруженность новых рабочих была на том же уровне, что и старых.
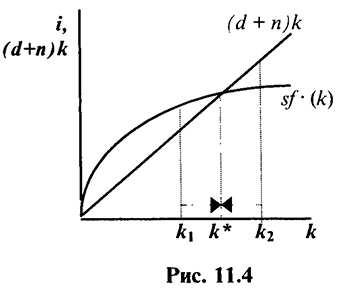
Условие устойчивого равновесия в экономике при неизменной фондовооруженности 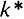 можно будет записать теперь так:
можно будет записать теперь так:
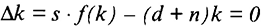
или
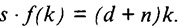
Данное состояние характеризуется полной занятостью ресурсов (рис. 11.4).
В устойчивом состоянии экономики капитал и выпуск на одного занятого, т.е. фондовооруженность (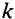 ) и производительность (
) и производительность (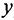 ) труда, остаются неизменными. Но, чтобы фондовооруженность оставалась постоянной и при росте населения, капитал должен возрастать с тем же темпом, что и население, т.е.
) труда, остаются неизменными. Но, чтобы фондовооруженность оставалась постоянной и при росте населения, капитал должен возрастать с тем же темпом, что и население, т.е.
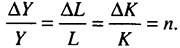
Таким образом, рост населения становится одной из причин непрерывного роста общего объема выпуска в условиях равновесия.
Отметим, что с увеличением темпа роста населения возрастает угловой коэффициент кривой 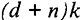 , что приводит к уменьшению равновесного уровня фондовооруженности
, что приводит к уменьшению равновесного уровня фондовооруженности 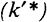 , а следовательно, к падению
, а следовательно, к падению 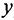 .
.
Учет в модели Солоу технологического прогресса видоизменяет исходную производственную функцию. Предполагается трудосберегающая форма технологического прогресса. Производственная функция будет представлена как 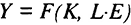 , где
, где 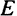 — эффективность единицы труда, зависящая от состояния здоровья, образования и квалификации работника, а
— эффективность единицы труда, зависящая от состояния здоровья, образования и квалификации работника, а 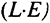 — численность условных единиц труда с постоянной эффективностью Чем выше тем больше продукции может быть произведено данным числом работников. Предполагается, что технологический прогресс осуществляется путем роста эффективности труда
— численность условных единиц труда с постоянной эффективностью Чем выше тем больше продукции может быть произведено данным числом работников. Предполагается, что технологический прогресс осуществляется путем роста эффективности труда 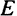 с постоянным темпом
с постоянным темпом 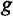 . Рост эффективности труда в данном случае аналогичен по результатам росту численности занятых: если технологический прогресс имеет темп
. Рост эффективности труда в данном случае аналогичен по результатам росту численности занятых: если технологический прогресс имеет темп 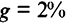 , то, например, 100 рабочих могут произвести столько же продукции, сколько ранее производили 102 рабочих. Если теперь численность занятых
, то, например, 100 рабочих могут произвести столько же продукции, сколько ранее производили 102 рабочих. Если теперь численность занятых 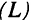 растет с темпом
растет с темпом 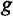 , а
, а 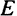 растет с темпом
растет с темпом 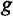 , то
, то 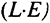 будет увеличиваться с темпом
будет увеличиваться с темпом 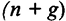 .
.
Включение технологического прогресса несколько меняет и анализ состояния устойчивого равновесия, хотя ход рассуждений сохраняется. Если определить 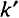 как количество капитала в расчете на единицу труда с постоянной эффективностью, т.е.
как количество капитала в расчете на единицу труда с постоянной эффективностью, т.е.
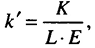
и
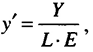
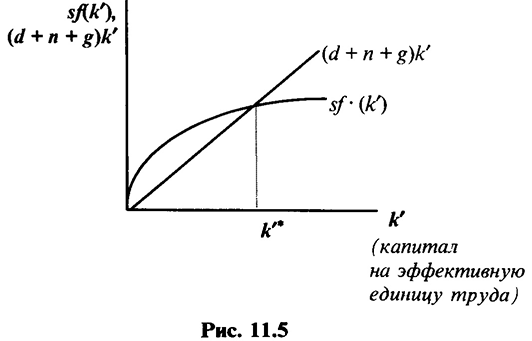
то результаты роста эффективных единиц труда аналогичны росту численности занятых (увеличение количества единиц труда с постоянной эффективностью снижает величину капитала, приходящегося на одну такую единицу). В состоянии устойчивого равновесия (рис. 11.5) уровень фондовооруженности 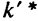 уравновешивает, с одной стороны, влияние инвестиций, повышающих фондовооруженность, а с другой стороны, воздействие выбытия, роста числа занятых и технологического прогресса, снижающих уровень капитала в расчете на эффективную единицу труда:
уравновешивает, с одной стороны, влияние инвестиций, повышающих фондовооруженность, а с другой стороны, воздействие выбытия, роста числа занятых и технологического прогресса, снижающих уровень капитала в расчете на эффективную единицу труда:
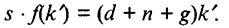
В устойчивом состоянии 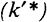 при наличии технологического прогресса общий объем капитала
при наличии технологического прогресса общий объем капитала 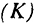 и выпуска
и выпуска 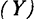 будут
будут
расти с темпом 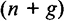 . Но, в отличие от случая роста населения, теперь будут расти с темпом
. Но, в отличие от случая роста населения, теперь будут расти с темпом 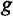 фондовооруженность
фондовооруженность 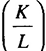 и выпуск
и выпуск 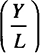 в расчете на одного занятого; последнее может служить основой для повышения благосостояния населения. Технологический прогресс в модели Солоу является, следовательно, единственным условием непрерывного роста уровня жизни, поскольку лишь при его наличии наблюдается устойчивый рост выпуска на душу населения
в расчете на одного занятого; последнее может служить основой для повышения благосостояния населения. Технологический прогресс в модели Солоу является, следовательно, единственным условием непрерывного роста уровня жизни, поскольку лишь при его наличии наблюдается устойчивый рост выпуска на душу населения 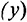 .
.
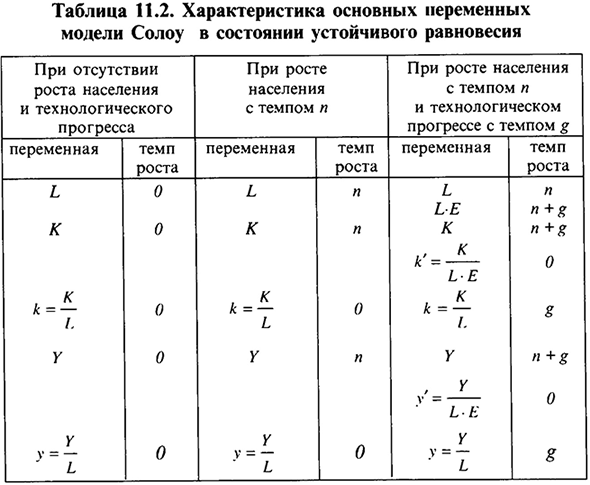
Таким образом, в модели Солоу найдено объяснение механизма непрерывного экономического роста в режиме равновесия при полной занятости ресурсов.
Как известно, в кейнсианских моделях норма сбережения задавалась экзогенно и определяла величину равновесного темпа роста дохода. В неоклассической модели Солоу при любой норме сбережения рыночная экономика стремится к соответствующему устойчивому уровню фондовооруженности (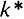 ) и сбалансированному росту, когда доход и капитал растут с темпом
) и сбалансированному росту, когда доход и капитал растут с темпом 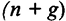 . Величина нормы сбережения (накопления) является объектом экономической политики и важна при оценке различных программ экономического роста.
. Величина нормы сбережения (накопления) является объектом экономической политики и важна при оценке различных программ экономического роста.
Поскольку равновесный экономический рост совместим с различными нормами сбережения (как мы видели, увеличение 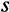 лишь на короткое время ускоряло рост экономики, в длительном же периоде экономика возвращалась к устойчивому равновесию и постоянному темпу роста в зависимости от значений
лишь на короткое время ускоряло рост экономики, в длительном же периоде экономика возвращалась к устойчивому равновесию и постоянному темпу роста в зависимости от значений 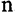 и
и 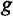 ), возникает проблема выбора оптимальной нормы сбережения.
), возникает проблема выбора оптимальной нормы сбережения.
Оптимальная норма накопления, соответствующая «золотому правилу» Э. Фелпса, обеспечивает равновесный экономический рост с максимальным уровнем потребления. Устойчивый уровень фондовооруженности, соответствующий этой норме накопления, обозначим 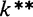 , а потребления —
, а потребления — 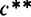 .
.
Уровень потребления в расчете на одного занятого при любом устойчивом значении фондовооруженности 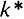 определяется путем ряда преобразований исходного тождества:
определяется путем ряда преобразований исходного тождества:
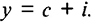
Выражаем потребление 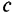 через
через 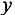 и
и 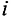 и подставляем значения данных параметров, которые они принимают в устойчивом состоянии:
и подставляем значения данных параметров, которые они принимают в устойчивом состоянии:
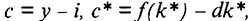
где 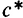 — потребление в состоянии устойчивого роста, a
— потребление в состоянии устойчивого роста, a
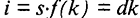
по определению устойчивого уровня фондовооруженности. Теперь из различных устойчивых уровней фондовооруженности (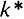 ), соответствующих разным значениям
), соответствующих разным значениям 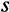 , необходимо выбрать такой, при котором потребление достигает максимума (рис. 11.6).
, необходимо выбрать такой, при котором потребление достигает максимума (рис. 11.6).
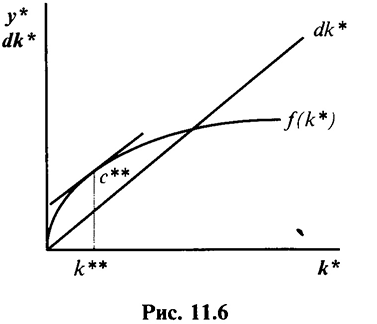
Если выбрано 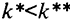 , то объем выпуска увеличивается в большей степени, чем величина выбытия (линия
, то объем выпуска увеличивается в большей степени, чем величина выбытия (линия 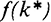 на графике круче, чем
на графике круче, чем 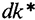 ), а значит, разница между ними, равная потреблению, растет. При
), а значит, разница между ними, равная потреблению, растет. При 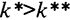 увеличение объема выпуска меньше роста выбытия, т.е. потребление падает. Рост потребления возможен лишь до точки
увеличение объема выпуска меньше роста выбытия, т.е. потребление падает. Рост потребления возможен лишь до точки 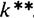 , где оно достигает максимума (производственная функция и кривая
, где оно достигает максимума (производственная функция и кривая 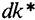 имеют здесь одинаковый наклон).
имеют здесь одинаковый наклон).
В этой точке увеличение запаса капитала на единицу даст прирост выпуска, равный предельному продукту капитала (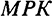 ), и увеличит выбытие на величину
), и увеличит выбытие на величину 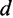 (износ на единицу капитала). Роста потребления не будет, если весь прирост выпуска будет использован на увеличение инвестиций для покрытия выбытия. Таким образом, при уровне фондовооруженности, соответствующем «золотому правилу» (
(износ на единицу капитала). Роста потребления не будет, если весь прирост выпуска будет использован на увеличение инвестиций для покрытия выбытия. Таким образом, при уровне фондовооруженности, соответствующем «золотому правилу» (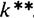 ), должно выполняться условие:
), должно выполняться условие: 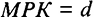 (предельный продукт капитала равен норме выбытия), а с учетом роста населения и технологического прогресса:
(предельный продукт капитала равен норме выбытия), а с учетом роста населения и технологического прогресса:
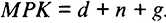
Если экономика в исходном состоянии имеет запас капитала больший, чем следует по «золотому правилу», необходима программа по снижению нормы накопления. Эта программа обусловливает увеличение потребления и снижение инвестиций. При этом экономика выходит из состояния равновесия и вновь достигает его при пропорциях, соответствующих «золотому правилу».
Если экономика в исходном состоянии имеет запас капитала меньше, чем 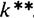 , необходима программа, направленная на повышение нормы сбережения. Эта программа первоначально приводит к росту инвестиций и падению потребления, но по мере накопления капитала с определенного момента потребление вновь начинает расти. В результате экономика достигает нового равновесия, но уже в соответствии с «золотым правилом», где потребление превышает исходный уровень. Данная программа обычно считается непопулярной в связи с наличием «переходного периода», характеризующегося падением потребления, поэтому ее принятие зависит от межвременных предпочтений политиков, их ориентации на краткосрочный или долгосрочный результат.
, необходима программа, направленная на повышение нормы сбережения. Эта программа первоначально приводит к росту инвестиций и падению потребления, но по мере накопления капитала с определенного момента потребление вновь начинает расти. В результате экономика достигает нового равновесия, но уже в соответствии с «золотым правилом», где потребление превышает исходный уровень. Данная программа обычно считается непопулярной в связи с наличием «переходного периода», характеризующегося падением потребления, поэтому ее принятие зависит от межвременных предпочтений политиков, их ориентации на краткосрочный или долгосрочный результат.
Рассмотренная модель Солоу позволяет описать механизм долгосрочного экономического роста, сохраняющий равновесие в экономике и полную занятость факторов. Она выделяет технический прогресс как единственную основу устойчивого роста благосостояния и позволяет найти оптимальный вариант роста, обеспечивающий максимум потребления.
Представленная модель не свободна и от недостатков. Модель анализирует состояния устойчивого равновесия, достигаемые в длительной перспективе, тогда как для экономической политики важна и краткосрочная динамика производства и уровня жизни. Многие экзогенные переменные модели Солоу — 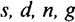 -предпочтительнее было бы определять внутри модели, поскольку они тесно связаны с другими ее параметрами и могут видоизменять конечный результат.
-предпочтительнее было бы определять внутри модели, поскольку они тесно связаны с другими ее параметрами и могут видоизменять конечный результат.
Модель не включает также целый ряд ограничителей роста, существенных в современных условиях ресурсных, экологических, социальных. Используемая в модели функция Кобба-Дугласа, описывая лишь определенный тип взаимодействия факторов производства, не всегда отражает реальную ситуацию в экономике. Эти и другие недостатки пытаются преодолеть современные теории экономического роста.
В неоклассической модели роста объем выпуска в устойчивом состоянии растет с темпом 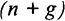 , а выпуск на душу населения — с темпом
, а выпуск на душу населения — с темпом 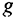 , т.е. устойчивый темп роста определяется экзогенно. Современные теории эндогенного роста пытаются определить устойчивый темп роста в рамках модели, эндогенно, связывая его со всеми возможными количественными и качественными факторами: ресурсными, институциональными и др.
, т.е. устойчивый темп роста определяется экзогенно. Современные теории эндогенного роста пытаются определить устойчивый темп роста в рамках модели, эндогенно, связывая его со всеми возможными количественными и качественными факторами: ресурсными, институциональными и др.
Сторонники концепции «экономики предложения» полагают, что увеличение темпов роста при полной занятости возможно прежде всего путем сокращения регулирующего вмешательства извне в рыночную систему.
Эта лекция взята со страницы решения задач по макроэкономике:
Решение задач по макроэкономике
Возможно эти страницы вам будут полезны:

