Оглавление:
Необходимый признак сходимости ряда
Теорема. Если ряд (1) сходится, то его общий член стремится к нулю, т. е.
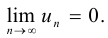
Следствие. Если 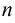 -й член ряда не стремится к нулю при
-й член ряда не стремится к нулю при 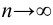 , то ряд расходится.
, то ряд расходится.
Задача №104.
Записать первые пять членов ряда, общий член которого задан формулой 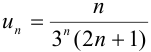 .
.
Решение:
Полагая в данной формуле 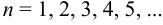 , получаем:
, получаем:
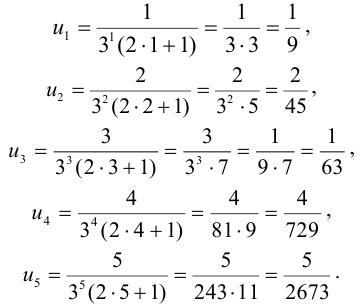
Следовательно,
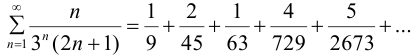
Задача №105.
Найти формулу для общего члена ряда 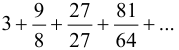
Решение:
Каждый член данного ряда представляет собой дробь, числитель которой — степень числа 3, а знаменатель — третья степень числа 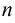 , т. е.
, т. е. 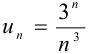 .
.
Числовые ряды
Числовым рядом называется выражение вида

Числа 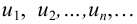 называются членами ряда, а
называются членами ряда, а 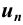 — общий член ряда.
— общий член ряда.
Конечная сумма 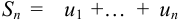 называется
называется 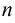 -й частичной суммой ряда.
-й частичной суммой ряда.
Конечный предел частичной суммы ряда при 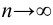 называется суммой ряда
называется суммой ряда
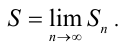
Ряд, имеющий конечную сумму 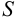 , называется сходящимся.
, называется сходящимся.
Если 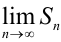 не существует или равен бесконечности, то ряд называется расходящимся.
не существует или равен бесконечности, то ряд называется расходящимся.
Если в ряде (1) отбросить первые 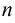 членов, то получится ряд
членов, то получится ряд
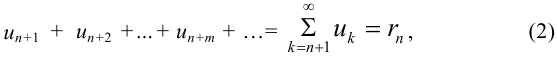
называемый остатком ряда (1) после 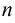 -го члена или
-го члена или 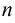 -м остатком.
-м остатком.
Если сходится ряд (1), то сходится и любой из его остатков (2).
Из сходимости остатков (2) следует сходимость ряда (1).
Простейшими примерами числовых рядов являются ряды:
1) геометрический ряд
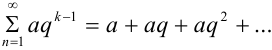 , при
, при 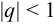 ряд сходится;
ряд сходится;
2) ряд Дирихле
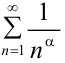 при
при 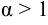 ряд сходится, при
ряд сходится, при 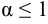 расходится.
расходится.
Если 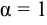 , то ряд называется гармоническим.
, то ряд называется гармоническим.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

