Оглавление:
Помимо свойств рядов важными механизмами в установлении сходимости или расходимости ряда без использования последовательности его частичных сумм являются специальные признаки сходимости. Первый из них — необходимый признак сходимости. Приведем его без доказательства.
Необходимый признак сходимости ряда: если ряд 
сходится, то его общий член стремится к нулю, т.е. 
.
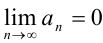Условие стремления общего члена ряда к нулю является необходимым, но не достаточным условием сходимости ряда. Для того чтобы в этом убедиться, надо привести пример расходящегося ряда, общий член которого стремится к нулю. Примером такого ряда может служить гармонический ряд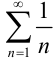 
. Действительно, 
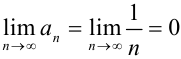, однако данный ряд расходится (доказательство этого опустим). Поэтому, если общий член ряда стремится к нулю, то о сходимости или расходимости ряда заранее ничего сказать нельзя.
На практике часто используется эквивалентное необходимому условию сходимости достаточное условие расходимости ряда: если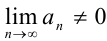 
или вовсе нс существует, то ряд расходится.
Пример №32.6.
Проверьте, выполняется ли необходимый признак сходимости для ряда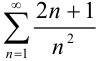 
.
Решение:
Найдем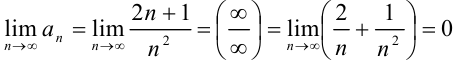 
. Следовательно, необходимый признак сходимости ряда выполняется. Однако, для установления сходимости (расходимости) ряда требуются дополнительные исследования.
Ответ: необходимый признак сходимости для ряда 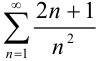выполняется.
Пример №32.7.
Исследуйте ряд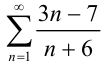 
на сходимость.
Решение:
Найдем
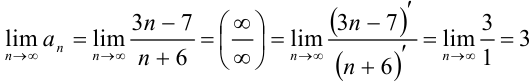(при раскрытии неопределенности 
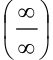использовали правило Лопиталя). Итак, 
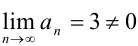(необходимый признак сходимости для ряда 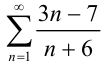не выполняется). Таким образом, в силу достаточного условия расходимости, исследуемый ряд расходится.
Ответ: 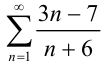расходится.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Определение числового ряда. |
| Свойства числовых рядов. |
| Признак сравнения. |
| Признак Даламбсра. |
