Необходимое условие существования экстремума функции даёт теорема Ферма:
Теорема Ферма. Если точка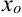 
— точка экстремума функции 
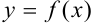и в ней существует производная 
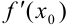, то эта производная равна нулю, т.e. 
.
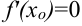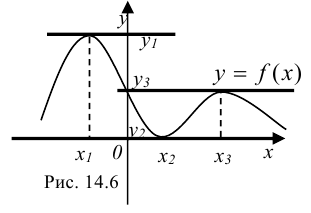
Эта теорема имеет простой геометрический смысл (рис. 14.6): касательные, проведенные к графику функции в точках экстремума (при условии существования в них производной, а, следовательно, единой касательной), параллельны оси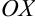 
. Угловой коэффициент 
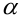касательных, проведенных к графику функции в точках экстремума, равен 0, и в силу геометрического смысла производной (
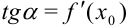), производная функции в этих точках обращается в ноль.
Точки, в которых производная функции равна нулю или не существует, назовем критическими точками (первого рода). Только среди критических точек могут быть точки экстремума.
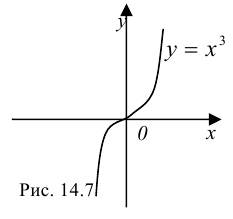
Но любая ли критическая точка является точкой экстремума? Рассмотрим всем хорошо известную функцию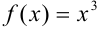 
. Найдем ее производную 
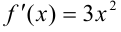и критические точки: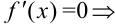 
.
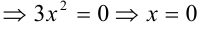Итак,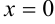 
является критической точкой функции 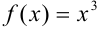, но она не является точкой экстремума. Таким образом, теорема Ферма дает только необходимые условия существования экстремума.
Чтобы выяснить, в каких критических точках функция имеет экстремум, рассмотрим достаточные условия существования экстремума.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Признаки возрастания и убывания функции |
| Понятие точек экстремума и экстремумов функции |
| Достаточные условия существования экстремума |
| Понятие выпуклой и вогнутой функции |
