Необходимые и достаточные условия оптимума в задачах математического программирования
В общем случае в задачах математического программирования ставится вопрос об отыскании локального минимума (максимума) целевой функции, т.е. такого значения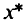 
, при котором для значений 
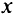, принадлежащих некоторой окрестности этого значения 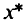, выполняются неравенства 
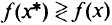для строго минимума (максимума) и 
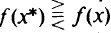для нестрогого минимума (максимума). Как и для функций одной переменной, в задачах математического программирования требуется сформулировать необходимые и достаточные условия существования оптимума. Если в задаче математического программирования множество 
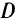выпукло, а функция 
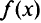дифференцируема в точке 
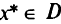то градиент 
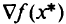, если он отличен от нуля, составляет нетупой угол 
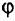с вектором, направленным из 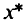в любую точку 
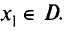. Другими словами, скалярное произведение 
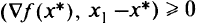(рис. 1.7). Для точки 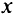не являющейся решением задач и, всегда найдется такая точка 
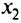, что угол 
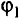, будет больше 
.
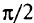В тех случаях, когда решение 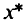принадлежит внутренней области 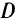, градиент 
.
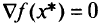Сформулированное условие является необходимым условием локальной оптимальности в задаче минимизациидифференцируемой функции на выпуклом множестве (для выпуклой задачи оно является и достаточным условием глобальной оптимальности).
Для области 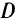в виде параллелепипеда, когда
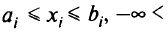
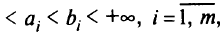
данное (необходимое) условие следует понимать как
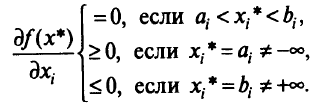
Здесь градиент «смотрит» внутрь области .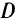
Чтобы определить координаты возможной оптимальной точки, надо из необходимых условий составить соответствующие системы уравнений и решить их.
В общем случае для задачи вида
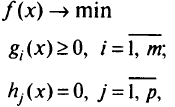
вводится функция Лагранжа
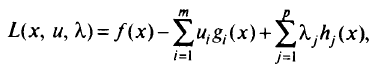
где
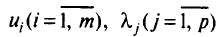
множители Лагранжа, подлежащие определению наряду с координатами векторах. Множители Лагранжа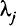 
для ограничений-равенств могут иметь любой знак, множители Лагранжа 
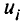для ограничений-неравенств — неотрицательны. Если в задаче математического программирования (1.4)—(1.6) множество 
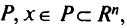выпукло, функции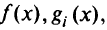 
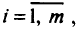выпуклы на 
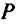и дифференцируемы в точке
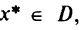
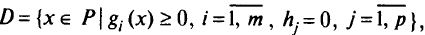
функции
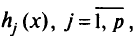
линейны, и для некоторых
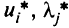
выполняются условия
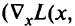
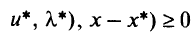
при всех
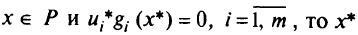
(глобальное) решение этой задачи. Соотношения
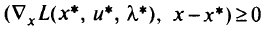
при всех
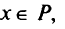
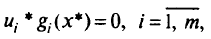
для задачи выпуклого программирования являются не только необходимыми, но и достаточными условиями существования решения (условия Куна-Таккера):
а) если 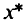является внутренней точкой области
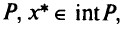
то условие (1.8) эквивалентно
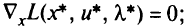
б) если область 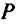имеет вид параллелепипеда
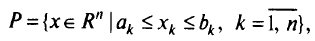
где
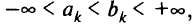
то соотношение (1.8) эквивалентно следующему условию:
для любого
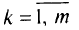
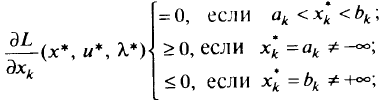
в) если 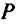учитывает условие неотрицательности части 
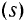переменных и имеет вид
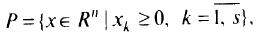
где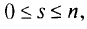 
то условие (1.8) эквивалентно совокупности условий:
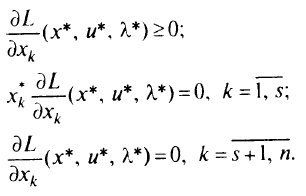
В отличие от методов отыскания оптимальных решений в задачах безофаничений-неравенств здесь появляется дополнительное условие (1.9), которое называют условием дополняющей не-жесткости:
Это условие разделяет ограничения-неравенства на активные, которые в точке оптимума обращаются в нуль
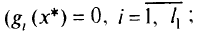
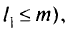
и пассивные
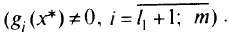
Для пассивных ограничений коэффициенты Лагранжа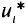 
должны быть равны нулю, при этом пассивные ограничения не оказывают своего влияния на решение 
.
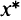Рассмотрим случай, когда в функции Лагранжа присутствуют только ограничения-неравенства:
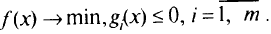
Тогда в точке минимума
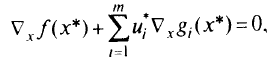
т.е. антиградиент целевой функции является неотрицательной линейной комбинацией градиентов функций, образующих активные ограничения в точке 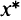(рис. 1.8).
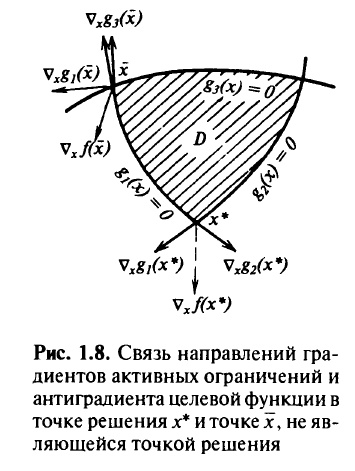
На рис. 1.8 показано множество, образованное неравенствами
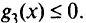
Здесь же в точках 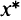и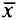 
указаны направления градиентов активных ограничений и антиградиента целевой функции. Отсюда следует, что точкой оптимума не может быть точка 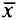так как в ней не выполняется условие того, что антиградиент 
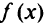есть положительная линейная комбинация градиентов активных ограничений. Решением является точка 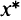, где данное условие выполняется.
Мы рассмотрели некоторые условия существования решения, учтя производные первого порядка. Как и для функции одной переменной при анализе условий оптимальности можно рассматривать производные высших порядков (в частности, второго). В задачах математического программирования сформулированы и доказаны условия оптимальности второго порядка, в которых оперируют вторыми частными производными от функции Лагранжа. Здесь мы их рассматривать не будем.
В общем случае задачу математического программирования можно было бы решать по следующей схеме:
- Запись задачи в канонической форме вида (1.4)—(1.6) и составление функции Лагранжа (1.7).
- Составление системы условий, которые характеризуют решение (определяют точки, где возможно существование оптимального решения — стационарные точки): в развернутой форме записывают условия (1.8), (1.9), а также условия, накладываемые задачей на допустимые значения и на множители Лагранжа. Например, для условия (1.10) полная система для определения стационарных точек имеет вид:
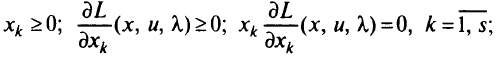
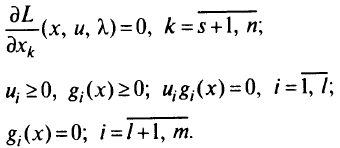
- Решение полученной системы необходимых условий. Это удается сделать в аналитическом виде лишь в редких случаях.
- Если удалось получить решение системы необходимых условий т.е. получены стационарные точки, надо провести исследование стационарных точек для отбора среди них решений. Это тоже сделать непросто. Иногда проще провести непосредственное исследование поведения целевой функции в стационарной точке.
На последних двух этапах полезно привлечение физических и геометричских соображений о возможном решении задачи математического программирования.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
