Оглавление:
Необходимые и достаточные условия локального экстремума функции двух переменных
Определение 21.1. Функция 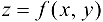 имеет локальный максимум (минимум) в точке
имеет локальный максимум (минимум) в точке 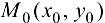 , если существует
, если существует 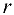 -окрестность данной точки, такая, что для всех точек этой окрестности выполняется неравенство
-окрестность данной точки, такая, что для всех точек этой окрестности выполняется неравенство 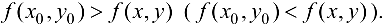 .
.
Пример 21.1.
Функция 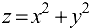 достигает минимума в точке
достигает минимума в точке 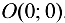 .
.
Теорема 21.1 *(необходимые условия экстремума). Если функция 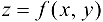 имеет экстремум в точке
имеет экстремум в точке 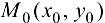 , то каждая частная производная первого порядка данной функции или обращается в этой точке в нуль, или не существует.
, то каждая частная производная первого порядка данной функции или обращается в этой точке в нуль, или не существует.
Так же, как и в случае функции одной переменной, точки, в которых частные производные обращаются в пуль или не существуют, называются критическими (стационарными) точками функции 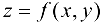 .
.
Теорема 21.2* (достаточные условия экстремума). Пусть функция 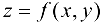 определена и имеет непрерывные частные производные второго порядка в некоторой области D. Пусть точка
определена и имеет непрерывные частные производные второго порядка в некоторой области D. Пусть точка 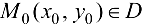 — критическая точка функции
— критическая точка функции 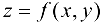 . Обозначим
. Обозначим
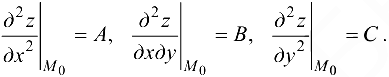
Тогда, если
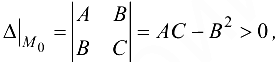
то в точке 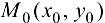 функция
функция 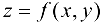 имеет экстремум, причем если
имеет экстремум, причем если 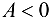 — максимум, если
— максимум, если 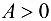 — минимум;
— минимум;
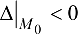 — функция экстремума не имеет;
— функция экстремума не имеет;
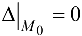 -необходимы дополнительные исследования.
-необходимы дополнительные исследования.
Заметим, что в случае 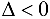 , т. е. когда в точке
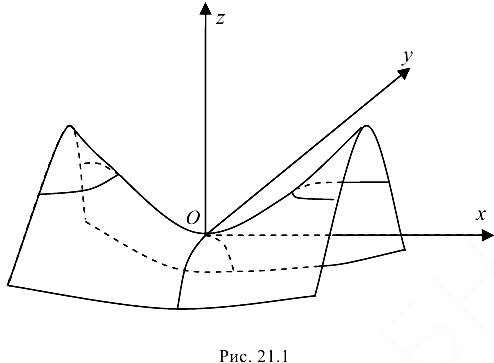
, т. е. когда в точке 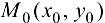 функция не имеет ни минимума, ни максимума, поверхность, служащая графиком функции, может вблизи этой точки иметь форму «седла». Например,
функция не имеет ни минимума, ни максимума, поверхность, служащая графиком функции, может вблизи этой точки иметь форму «седла». Например, 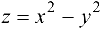 (рис. 21.1). В этом случае говорят, что в данной точке наблюдается явление минимакса.
(рис. 21.1). В этом случае говорят, что в данной точке наблюдается явление минимакса.
Теорема 21.3* (достаточные условия экстремума). Пусть функция 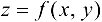 определена и имеет непрерывные частные производные второго порядка в некоторой области D. Пусть точка
определена и имеет непрерывные частные производные второго порядка в некоторой области D. Пусть точка 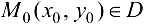 — критическая точка функции
— критическая точка функции 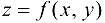 . Тогда, если:
. Тогда, если:
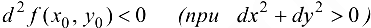 , то в точке
, то в точке 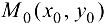 функция
функция 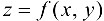 имеет максимум;
имеет максимум;
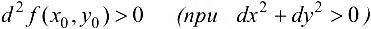
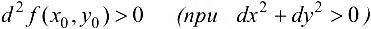 . то в точке
. то в точке 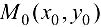 функция
функция 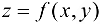 имеет минимум.
имеет минимум.
Пример 21.2.
Исследовать на экстремум функцию
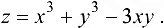
Решение:
Используя необходимые условия экстремума, найдем критические точки. Для этого найдем частные производные первого порядка
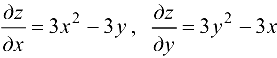
и решим систему уравнений
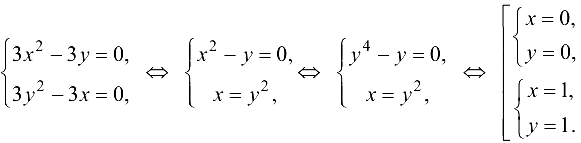
Таким образом, получены две критические точки 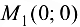 и
и 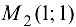 .
.
Для исследования характера критических точек найдем частные производные второго порядка 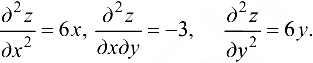
Тогда 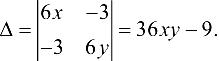 .
.
Для точки 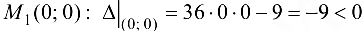 , т. е. в этой точке функция не имеет экстремума.
, т. е. в этой точке функция не имеет экстремума.
Для точки 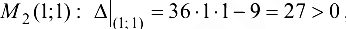 , т. е. в этой точке функция имеет экстремум, причем
, т. е. в этой точке функция имеет экстремум, причем 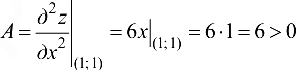 , следовательно, это минимум.
, следовательно, это минимум.
Вычислим 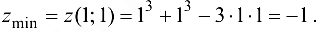
Если для определения характера экстремума использовать дифференциал второго порядка, то рассуждения будут следующие. Для данной функции
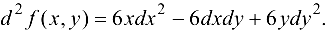
Тогда
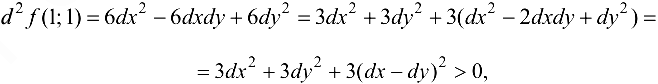
т. e. еще раз показано, что в точке 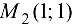 функция имеет минимум.
функция имеет минимум.
Ответ: 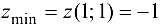 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

