Необходимые условия экстремума

Оглавление:

Необходимые условия экстремума

Необходимые условия экстремума. Вопросы, рассмотренные в этом и некоторых из нижеприведенных параграфов, являются аналитическими, и увеличение числа переменных не делает эти доказательства более сложными. Таким образом,§ 401 является экстремальным значением функции многих переменных Двадцать Мы рассмотрим их сразу в случае общих n-измерений, указав, при необходимости, некоторые особенности в случае n = 2 и n = 3. Определение 1.Определить функции Е (Х) в наборах и по. Точка x {0] eназывается называется точной минимальной минимальной максимальной точкой, если существует окрестность I /(x (0)) x (0) соответственно. Для всех x∈II(x(0)) Å, , φφ ’0} неравенство f(x)[(x (0)) содержит неравенство f (x)/(x°) соответственно.

(Строгие) максимальные и минимальные тонкие точки функции называются (строгими) крайними точками. Людмила Фирмаль

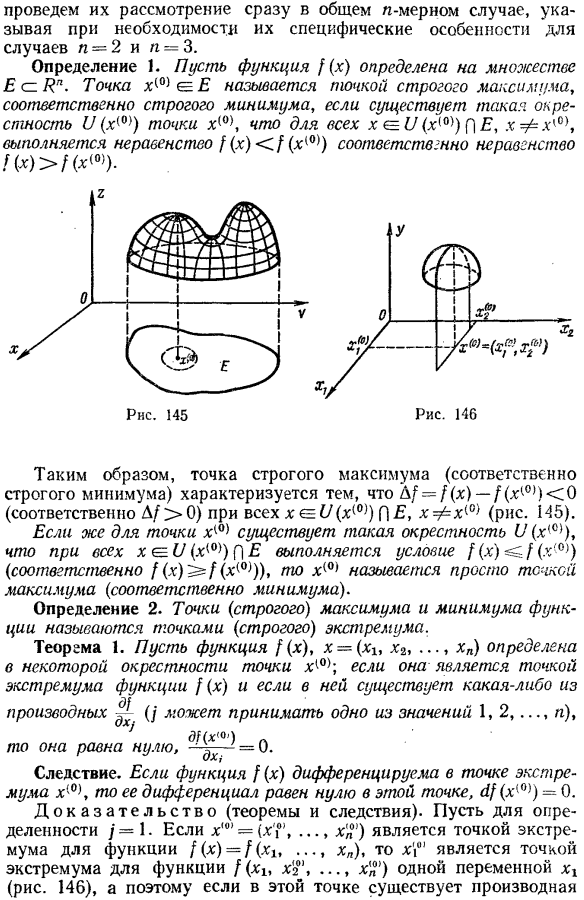
Итак, строгая максимальная точка (соответственно, строгая минимальная точка) характеризуется тем, что для каждого xe (//=/(x)-/(x10.) равно 0 (A/0, соответственно). xph {0 ’(рис. 145). Окрестность окрест (X ’ c}) существует в точке x (0), и все x > ((x(0)) conditions условия f (x)-C /(X.(1) ( | , соответственно) /(x)^ = /(x(0)), x (0) просто называется наибольшей точкой (наименьшей точкой, соответственно). Определение 2.Теорема 1.Функция f (x), x =(x1, x2,…предположим, вы определяете xn) в окрестности точки x (0). это экстремумы функции f (x)、 производные производные имеют значения 1, 2,…, n) может принимать любое значение и оно равно нулю、 дуплексный） 0.

Доказательство (Теорема и индуктивный метод). для уточнения пусть y = 1.если x10 ’==(Xx0′ x ’» 0′) это крайняя точка Функция f (x)= f (xx,…максимальное значение xn), то x) » это функция f (xx xr, в 1 переменной xx…, х)? (смотреть рисунок.146), следовательно, если в это время существует производная Если функция f (x) дифференцируема в крайней точке x10, то в этой точке все производные I-1, 2,…потому что, согласно тому, что n существует и доказано, все они равны нулю、 о□1-1. Образцы. 1.Найти крайнюю точку функции r = x2 + y2.

Если результирующая функция f(x) дифференцируема по экстремальному значению x°, то ее производная в этой точке равна нулю. Людмила Фирмаль

By доказано, что крайняя точка-это e? Он входит в крайнюю точку 2 = 0.Так как Λ= 2x axH-2 / y 1y, то условие π-0 выполняется в одной точке (0, 0).в этом отношении оно равно 2 = 0, а во всех остальных отношениях-2 = x2 +#2 0.So(0, 0) точная минимальная точка функции r = x2 + y2(рис.147). 2.Найти крайнюю точку функции r = x2-y%.Продолжая, как и в предыдущем случае, можно видеть, что условие π = 0 выполняется снова с точкой (0, 0) и эта точка 2= 0.Однако, здесь г = 0 и для любого xΦ0 есть 2 0, а для x = 0 и yφ0 есть Р0.Итак, точка(0, 0) не является экстремальной точки, поэтому функция Р-Х2-У2 имеет крайняя точка на всех(рис. 148).

Равномерная сходимость по параметру семейства функций.	Достаточные условия строгого экстремума.
Замечания о рядах Тейлора для функций многих переменных.	Замечания об экстремумах на множествах.