Необходимость
Пусть 
есть полный дифференциал, т. е.
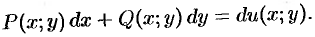
Учитывая, что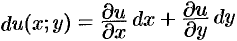 
(см. п. 44.3), имеем:
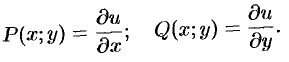
Дифференцируя эти равенства по 
и по 
соответственно, получаем
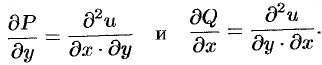
А так как смешанные частные производные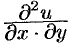 
и 
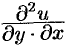равны
между собой (см. п. 44.2), получаем (48.19).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
