Оглавление:















Нелинейное программирование (планирование)
- Нелинейное программирование (планирование) Нелинейное программирование (планирование) — Математический метод определения максимального или минимального значения функции Ограничения на форму неравенств или уравнений. Максимизировать (минимизировать) функцию Представляет принятые критерии эффективности в решении проблем, Подходит для цели.
- Называется цель Функция. Ограничения характеризуют имеющиеся возможности Решение проблемы. Целевая функция или хотя бы одно ограничение являются нелинейными (То есть на графике нарисованы линии косвенных кривых). Сущность решения задач нелинейного программирования Это найти условия, чтобы полностью изменить цель Минимальная или максимальная функция.
Решения, отвечающие требованиям проблемы Достижение поставленной цели называется оптимальным планированием. Людмила Фирмаль
Выбор нелинейного программирования Оптимальное планирование для выделения ограниченных ресурсов Решение проблемы. В общем, постановки нелинейных задач Программирование сводится к следующему: Условия задания представлены с использованием системы Нелинейные уравнения или неравенства, представляющие ограничения, Взимается плата за использование доступных ресурсов: Ζ, (^ ,, ^ 2, …, χη)> 0; Ζ2 (, χ2, …, χη)> 0; Zm ( ,, * 2, …, xn)> 0 Если хх> 0, Где Ζ ,, Ζ2, …, Zm — соответствующие функции.
Условия (ограничения) для решения проблемы; χ-обязательные Количество, которое включает в себя решение проблемы. Целевая функция определяется следующим образом: y = f1 (*, x2, …, xn). (3,41) Кроме того, хотя бы одна из функций y, Ζ, 2, …, Zm- Нелинейная. Нелинейное программирование решено Проблема разнородного распределения ресурсов.
Есть м разных ресурсов Это должно быть реализовано для предприятий в регионе страны. Известная предполагаемая возможность (вероятность) Бизнес в j регионе (R.) и эффективность использования i-ro Ресурс p-й области (со). Распределение ресурсов по регионам характеризуется следующим образом: Управляющий параметр называется (ч.): О, если i-й ресурс не отправлен в j-й регион, [Если 1, ι- и ресурсы идут в j- и регион.
Вам нужно распределить ресурсы по регионам Сразу (выберите значение h) Возможность достижения цели greatest была наибольшей: N L Ι-Πθ-VO ;;) я = я = Макс Предел также должен быть соблюден. η ] ГЦ = 1, i = 1, 2, …, м. (3,42) (3,43) Этот предел применяется к каждому из m ресурсов Должен быть назначен в одном из регионов. Ниже приведен типичный набор задач, решаемых с помощью: Нелинейное программирование, чтобы объяснить это Возможности и решения.
Пример 3.5 Есть 4 разных типа владельцев Ресурсы, которые могут быть реализованы в четырех бизнесах Страна региона (t = η = 4). Предполагаемая возможность (вероятность) Начните бизнес в j регионе (R.) в указанной таблице. 3,16. Таблица 3 ] 6 Возможность начать бизнес в регионе область Вероятность (Pj) 1 0.2 2 0,4 3 0,3 4 0,1 Эффективность при использовании j-го ресурса i-ro Таблица заданной области (ω). 3,17.
Таблица 3.17 Эффективность использования ресурсов номер ресурс 1 2 3 4 Регион номер j 1 0,81 0,66 0,32 0,43 2 0,65 0,51 0,17 0,46 3 0,32 0,19 0,39 0,58 4 0,47 0,75 0,15 0,60 Вам необходимо выделить ресурсы для каждого такого региона Полная вероятность достижения цели деятельности (Успех) был самым большим. Кроме того, каждый ресурс Должны быть распространены во всех регионах.
Решения Рассмотрим самый простой случай в каждом случае Вы можете отправить только одну область поиска Unit. Проблемы нелинейного программирования Сводится к одному из частных случаев линейных задач Программирование. В то же время да Π (1-Ηϋωϋ) = 1-ΣΗϋωϋ ‘(3.44) я = я я = я Нт Ροδ = ΣΣ1ΐϋΡίωϋ ・ (3.45) j = l i = l В нашем случае m = n. Решение в этом случае Компиляция Ro матрицы A = || ||
Выберите из каждой строки и каждой строки 1 элемент столбца, всего Оказалось, самый большой. Это один из частных случаев линейного Программирование. Процедура расчета удобно выполняется с использованием: Следующий метод. Сначала вычисляются матричные элементы Α = || Ρ.ωϊ … 101 ||. Далее матрица А Конверсия. Самый большой элемент в каждом столбце Все элементы в этом столбце вычитаются из него.
Каждый ряд полученной матрицы Наименьший элемент найден и вычтен из всех элементов Эта строчка. Результирующая матрица обозначается A (0). На каждой строке В каждом столбце есть хотя бы один ноль. Первый столбец матрицы A (0) имеет ноль и Он помечен звездочкой. Затем второй столбец сканируется и В этом случае он помечается звездочкой ноль Тем не менее, нет нулевых строк со звездочкой.
Через все столбы цы. Полученный ноль со звездочкой называется независимым. R0) _ 0 0 78 28 30 56 117 0 * 41 135 0 * 3 76 76 0 15 Затем решение выполняется последовательно Аппроксимация (итерация). Каждый шаг итерации увеличивает число Ноль не зависит от каждой единицы. Тогда решение заканчивается Когда число независимых нулей равно n. Матрица A (0) имеет три независимых нуля, достаточно одного Итерация (η = 4 или более поздняя).
Итерации выполняются в следующем порядке: 1. Матрица A (0) (в общем случае Столбцы (в результате предыдущей итерации) отмечены знаком «+», Содержит независимые нули. Лежащие матричные элементы Выделенный столбец называется выделенным столбцом (см. Матрицу a ниже). 2. Проверьте, есть ли нули в невыбранных элементах.
Если да, перейдите к пункту 3. Если нет, перейдите к пункту 5. 3. Символ «» находится над неназначенным нулем. Проверьте, есть ли 0 * в строке, содержащей 0. Если есть, выделите его символом Удалите эту строку с помощью «+» (называется подсветкой) (кружок) Круг) Выделите отметку над столбцом, содержащим 0 * (см. Матрицу ниже) а). Затем вернитесь к шагу 2.
Если нет, перейдите к шагу 4. 4. Начиная с 0, строка на предыдущем шаге Так как 0 * был найден, построить цепочку, пока 0 * и 0 ‘чередуются Как можно дольше. Переход от 0 ‘к 0 * выполняется в последовательности, И вдоль линии от 0 * до 0 ‘(см. Матрицу c ниже). Звезды размещены на странных элементах цепочки, и Но они удалены.
Также количество независимых Ноль увеличивается на единицу. Все плюсы и штрихи уничтожены. Если число 0 * меньше n, вернитесь к шагу 1. Если η равно, переходите к шагу 6. 5. Самый маленький элемент выбирается из всех невыбранных элементов (В матрице он подчеркнут). Этот предмет будет вычтен из всего. Отменено и добавлено к элементу выше Пересечение выбранной строки и столбца (см. Матрицы a и b).
К следующему Переходите к шагу 2. 6. Оптимальное распределение поисковых систем установлено. Единица для каждого диапазона деятельности. Подходим эти места Матрица r с независимыми нулями. Максимальное значение P, равное сумме a, вычисляется. Стоя на независимой нулевой площадке. Последовательное преобразование матрицы A (0) Относящиеся к этому примеру (матрицы a, b, c, d) показаны ниже.
Независимая нулевая позиция матрицы r Оптимальное распределение ресурсов по регионам (Таблица 3.18). Таблица 3.18 Оптимальное распределение ресурсов по регионам номер ресурс 1 2 3 4 Номер региона 1 ] 2 1 — 3 — 1 4 — 1 Максимальное значение, соответствующее этому распределению Вероятность достижения цели равна сумме соответствующих Элементы матрицы А Ρ = 0,132 + 0,260 + 0,174 + 0,015 = 0,581.
Рассмотренный пример показывает случай, когда m = n. Если m m, ω = 0) Задача к рассматриваемому делу. Пример 3.6 Существуют две группы разнородных ресурсов (t = 2). Вы можете инвестировать в 3 инвестиционных проекта (n = 3). В первом Группа имеет 6 единиц ресурсов (N, = 6), а вторая -10 (N2 = 10). Важность проекта показана в таблице. 3,19. Таблица 3.19 Серьезность проекта [Проект Значение (Pj) 1 0,3 2 0.2 3 0,5
Эффективность вложения различных ресурсов (ωΓ) Данная таблица. 3,20. Таблица 3.20 Эффективность различных видов инвестиций в регионе Номер группы ресурсы 1 , 2 Номер проекта 1 0,40 0,20 2 0,10 0,40 3 0,50 0,20 Особенности распределения ресурсов проекта Матрица A = || x .. ||, где x. количество ресурсов типа -i-ro, Назначен на J-й проект.
Вы должны выделить ресурсы для таких проектов, как Для максимальной общей эффективности: = Макс j = l L i = l Должны быть соблюдены следующие ограничения: η 2 * ij = Nj; i = 1, 2, …, m; * y> 0, i = l, 2, …, m; j = l, 2, …, n (3,46) (3,47) Решения -Области, которые меняют максимальную функциональность Удовлетворительное начальное решение определяется Проблема ограничения.
- Использование специальных стандартов проверено, Является ли полученное решение достаточно близким к оптимальному. -Если полученное отклонение превышает требуемое значение, Построить так называемые возможные направления, Определение этого направления последнего шага является новым Возможное решение, которое увеличивает значение максимизации функция.
Процесс расчета соответствует Приблизительно и продолжаем несколько шагов Итеративное, почти оптимальное решение Приблизительная точность не требуется. Последовательность расчетов 1. Исходное жизнеспособное решение определяется И «> = || x„ w> ||, (3.48)
Где A (0) — матрица, характеризующая начальное распределение Ресурс проекта. Людмила Фирмаль
В качестве начального (начального) распространения вы можете: Любое (включая любое) распространение должно быть сделано (Матрица A (0)), нет противоречия Условие ограничения Задача. Чем это первоначальное распределение Когда это оптимально, требуется меньше итераций. Вы можете использовать приблизительные значения здесь Решение той же проблемы, полученной с использованием динамических методов Программирование (см. Далее в этом разделе).
Номер проекта (столбец) 12 три. II s o z iι A (0) = количество π групп ресурсов (строк) (3.49) Затем выполняется итеративный процесс. В результате Выполнение итерации дает k-е оптимальное k-е приближение Распределение: 2. Возможные компоненты матрицы Направления: S = ΣΑΓ = ΣΣ ^ Η ・ (3.54) j = l j = l V i = l) Количество A (k) сравнивается с количеством ε-требуется.
Отклонение математического ожидания, полученного на этом этапе (Общая эффективность) Из математического ожидания, Соответствует оптимальному распределению. Если A (k) <ε, решение почти оптимально d (10> ε_ Перейти к шагу 4. 4. Найдена длина \ шаг для запуска По возможному направлению, чтобы стать ближе к Лучшее решение Значение \ получается из уравнения η (м л ΣΧ ‘expUk £ aijS; /> U. j = l V i = l) 5.
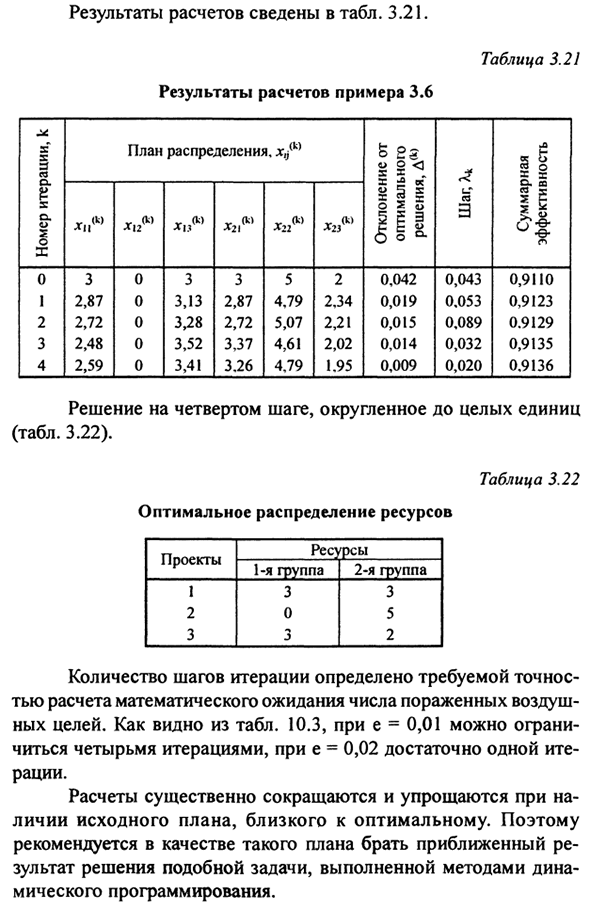
Найдено новое выполнимое решение A (k) v (k + 0 _ „(k) l« (k) X ) ~ ΧΪ) «» «^ k ^ ij Кроме того, расчет повторяется из пункта 2. = II г (к + 1> я (3,55) Где я (3,56) Результаты расчетов сведены в таблицу. 3,21. Таблица 3.21 Результат расчета примера 3.6 Номер итерации, 0 1 2 3 4 План распределения, х, джик) * р (к) 3 2,87 2,72 2,48 2,59 * 12 ° ° 0 0 0 0 0 против (К) 3 3,13 3,28 3,52 3,41 V (K) 3 2,87 2,72 3,37 3,26 Эй * 5 4,79 5,07 4,61 4,79 ^ (К) * 23 2 2, 34 2,21 2,02 1,95
Отклонение от оптимум Раствор, Δ00 0042 0,019 0,015 0,014 0,009 И.Г. но 0043 0053 0089 0032 0020 общая сумма КПД 0,9110 0,9123 0,9129 0,9135 0,9136 Решение на четвертом шаге, округленное до целого (Таблица 3.22). Таблица 3.22 Оптимальное распределение ресурсов Проект 1 2 3 Ресурс 1 Первая группа 3 0 3 Вторая группа 1 3 5 2 Дж Количество шагов итерации зависит от того, что вам нужно.
Точность расчета математического ожидания числа пострадавших Воздушная цель. Как видно из таблицы. 10,3, возможно, если е = 0,01 Если е = 0,02, достаточно одного. Повторить. Когда расчеты значительно сокращены и упрощены Почти оптимальная доступность оригинального плана. так Рекомендуется принять приближение в качестве такого плана Результат решения аналогичной задачи, выполненной методом Динамическое программирование.
Пример 3.7 Два деловых партнера решили совместно инвестировать Enterprise. Может выносить суждения на основе предыдущего опыта Вероятность успеха для обоих партнеров (P = 0,5, P2 = 0,3) и около Величина (доля) возможных денежных потерь (С, = 0,8, С2 = 0,4). Инвестиционные ограничения партнеров также известны: Минимальные инвестиции первого партнера а = 1 2-й а2 = 7 —
Максимальная сумма инвестиций первого партнера β = 2 Второй β2 = 10. Вероятность, необходимая для решения задачи W3 = 0,9, также приведена. Вам нужно найти лучшие инвестиции для обоих Партнеры x, opt и x ™ обеспечивают заранее определенную вероятность успеха, Минимизация потерь партнера (целевая функция): y = c, *, + c2x2. (3,57)
В этом случае необходимо учитывать ограничения α2 <χ2 <β2. (3,58) Решения Эта проблема так называемая Инкрементальный. Суть метода заключается в следующем: -Минимизация целевой функции (3,57) достигается. Последовательное приближение (итерация); -В качестве начального набора желаемых значений Переменная X0 = (x10, x, 0) Их минимальное значение a, a2 принято;
Каждый аргумент в первом шаге итерации Даны четкие приращения Ax10 и Δχ20. Состояние (3.61) — смотрите ниже. Результирующая переменная «Чистый» набор X, = (xi, x22); -X0 и X создают два «соединенных» набора. Один из аргументов является новым Значение. Второе значение не изменилось. -Инкремент на втором этапе Значение аргумента набора «join» основано на Лимит (3.61), опять «чистый» и новый.
Например, набор «присоединиться» -На каждом этапе чистого набора и набора комбинации По значению переменной вычисляется целевая функция y. Минимальное значение целевой функции на каждом «чистом» k-м шаге наем Утро этого шага и предыдущий шаг обозначается как yk Все через «присоединиться» -Y_k -Итерационный процесс Условие выполнено Λ-Ζκ-8 ‘(3,59) Где ε — точность, необходимая для решения проблемы (оценка потерь).
Последовательность расчетов 1. Исходный набор аргументов компилируется. Χ0 = (Χ.0 ^ 2θ) == (α.’α2) == (1’2) 2. Приращение аргумента Δχ. Принимает обратно пропорционально потере: т т Δχ10 = — = — = = l, 25т; 10 секунд, 0,8 Δχ, 0 = — = — = 2.5t. 20 С2 0,4 (3,60) Чтобы рассчитать значение т, используйте Формулы, полученные с использованием теории вероятностей (см. (Следующий абзац в этой главе): w3 = i to (i-p1) x, -a, (i-P2) r2 «a2. О ・ 6 *)
Присвойте значение, соответствующее выражению (3.61). W3 = 0,9 = 1- (l-0,5) x, «, (l-0,3) Jr2» 2; 0.1 = 0,1-0,5 * Η0,7 * 2-2> 0, Где Ζ — соответствующая неубывающая функция Ограничить. Параметр t определяется из граничных условий при Ζ = 0. Связанный индекс Значения Ax10 и Δχ20: Z = 0, l-0,5, ’25t-0,72’5t = 0 (3,62) Из уравнения (3.62), t = 1.21 и из уравнения (3.60) Αχϊ0 = 1,25 ・ 1,21 = 1,51; Ax20 = 2,5 ・ 1,21 = 3,02 3.
Первый шаг итерации выполнен. chi = ss, + Ad10 = 1 + 1,51 = 2,51; χ] 2 = α2 + Δχ20 = 2 + 3.02 = 5.02 Выявлено чистое множество X = (xi; x] 2) = (2,51; 5,02). Составляются два набора комбинаций (1.0; 5.02) и (2.51; 2.0). 4. Целевое значение рассчитывается по формуле (3.57) Функции чистого набора и комбинированного набора, две из них Последний выбирает минимальное значение: Для чистого набора y} = 0,8-2,51 n-0,4 5,02 = 4,02;
Комбинированный набор: Сначала y = 0,8 ・ 1 + 0,4 ・ 5,02 = 2,81; 2-й у = 0,8-2,51 н-0,4 ≤ 2,0 = 2,81; Y_x = минимум (2,81; 2,81) = 2,81. Ожидаемый потрясающий = 4,02-2,81 = 1,21. Первый шаг к решению этого Точность оценки потерь берется из чистого набора, х = 2,51; х2 = 5,02 или *, «3; х2» 5. Второй этап итерации выполняется так же, как и пункт 3. Найдены два чистых набора (1.87; 6.77) и (3.40; 3.79).
4 облигации (1,0; 6,77), (1,87; 5,02), (2,51; 3,79) и (3,40; 2,0). 5. Значения целевой функции рассчитываются для всех Сотрите второй набор шагов и выберите его минимальное значение Второй и первый предыдущий шаг: Первый набор y2 = 0,8-1,87 н-0,4 · 6,77 = 4,20. Второй набор y2 = 0,8 · 3,40 + 0,4 · 3,79 = 4,24. у2 = минимум (4,02; 4,20; 4,24) = 4,02 Значения целевой функции рассчитываются для всех.
Второй шаг и набор комбинаций выбора Его минимальное значение: Первый набор y2 = 0,8 · 1,0 + 0,4 · 6,77 = 3,50. Второй набор y2 = 0,8-1,87 + 0,4 · 5,02 = 3,51. Третий набор y2 = 0,8 · 2,51 + 0,4 · 3,79 = 3,53. Четвертый набор — y2 = 0,8 · 3,40 + 0,4 · 2,0 = 3,52. Y2 = минуты (3,50; 3,51; 3,53; 3,52) = 3,50. Расчетное yu2-y = 4,02-3,50 = 0,52 На втором этапе соответствующее решение Точность оценки потерь берется из чистого набора.
Меньше, χχ = 1,87. х2 = 6,11 или х2 «; х2» 7. На следующем шаге разница yk ~. Yk следует Она уменьшается. В этом случае вам нужно подтвердить, что вам нужно Капитал первого и второго партнера не превышал β, а β2 Соответственно. Когда капитал приобретен больше указанного Если есть предел, стоит обратить внимание на его крайнюю ценность. Когда точность потерь ограничена ε = 1% Для решения проблемы требуется еще три шага.
Смотрите также:
| Логические задачи и задачи на смекалку | Динамическое программирование (планирование) |
| Методы оптимизации: линейное программирование | Теория вероятностей и математическая статистика. Основные понятия |

