Нелинейная регрессия и корреляция
Подбор функции регрессии должен производиться с применением теории конкретной науки, на базе которой формулируется задача измерения связи между явлениями. При этом следует использовать методы выявления наличия связи. Односторонняя стохастическая зависимость может быть выражена и при помощи нелинейных функций. Различают два класса нелинейных регрессий. К первому классу относятся функции, нелинейные относительно факторного признака, но линейные относительно параметров, входящих в данные функции.
Для оценок параметров таких функций применяется метод наименьших квадратов, следовательно, остаются в силе все исходные предпосылки линейного регрессионного анализа. Второй класс регрессий характеризуется нелинейностью факторного признака, входящего в уравнение регрессии.
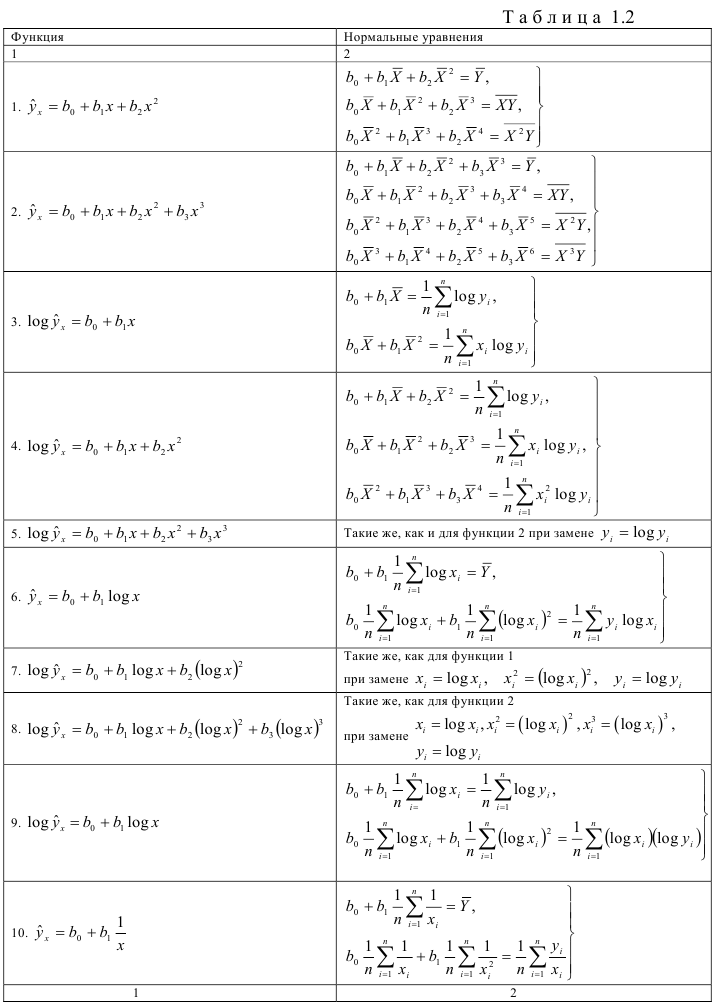

Функции, наиболее часто встречающиеся в однофакторных регрессионных моделях, представлены в табл. 1.2 (квазилинейные функции) и 1.3 (нелинейные функции второго класса), где даны также нормальные уравнения для определения входящих в них параметров и преобразованные функции (для нелинейных функций второго класса).
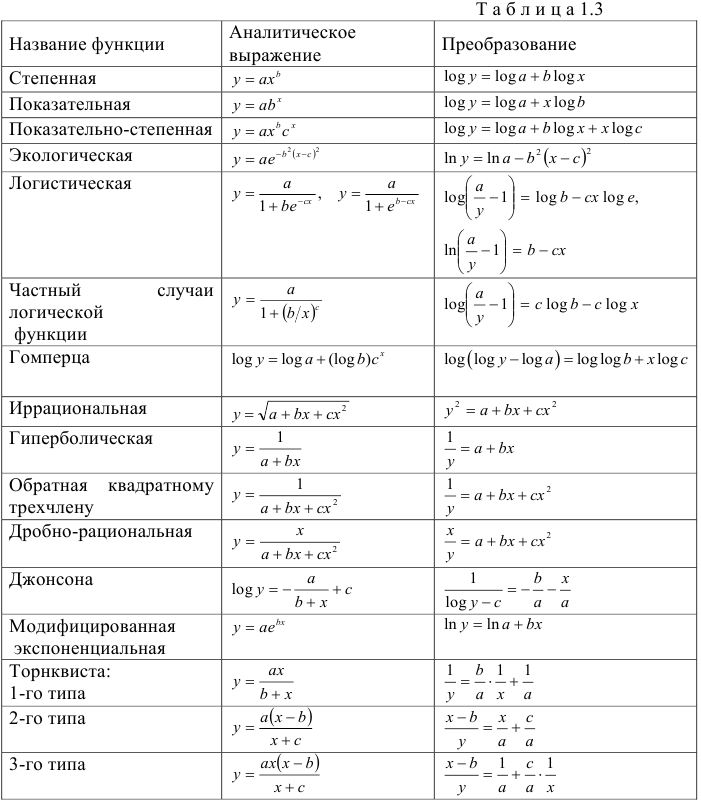
В табл. 1.2 и 1.3 указаны классы регрессий, характеризующихся нелинейностью относительно переменной  или относительно оцениваемых параметров. Квазилинейные функции (см. табл. 1.2) линейны относительно искомых параметров, т.е. их можно представить в виде
или относительно оцениваемых параметров. Квазилинейные функции (см. табл. 1.2) линейны относительно искомых параметров, т.е. их можно представить в виде
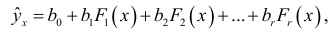
где 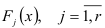 — функции переменной
— функции переменной 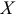 . Они не содержат параметров. Например,
. Они не содержат параметров. Например, 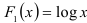 или
или 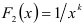 и т.д. Поэтому к функции (1.3) можно применить метод наименьших квадратов. Получим систему нормальных уравнений:
и т.д. Поэтому к функции (1.3) можно применить метод наименьших квадратов. Получим систему нормальных уравнений:
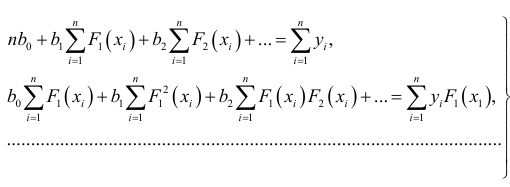
Правило составления нормальных уравнений системы состоит в следующем: первое уравнение системы получается суммированием функций 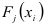 по
по 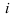 из уравнения (1.3), остальные уравнения — последовательным умножением функции регрессии (1.3) соответственно на
из уравнения (1.3), остальные уравнения — последовательным умножением функции регрессии (1.3) соответственно на 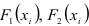 ,… и последующим суммированием полученных результатов по
,… и последующим суммированием полученных результатов по 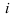 .
.
Для получения оценок параметров функций из табл. 1.3 их предварительно подвергают преобразованиям, главное назначение которых -линеаризация рассматриваемых зависимостей по оцениваемым параметрам. Параметры регрессии исходных функций находят путем обратных преобразований. Например, путем логарифмического преобразования можно перейти от зависимости показательного типа 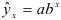 к линейной
к линейной
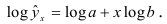
Применяя метод наименьших квадратов к функции
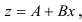
где
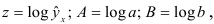
получаем значения
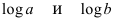
Потенцируя полученные значения, находим оценки параметров исходной функции.
Вычислив дисперсию результативного признака 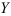 и воспользовавшись отклонениями величины
и воспользовавшись отклонениями величины 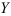 от средней величины
от средней величины 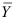 , получим показатель общей дисперсии
, получим показатель общей дисперсии 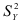 , характеризующей вариацию признака
, характеризующей вариацию признака 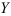 . Вычислив дисперсию
. Вычислив дисперсию 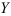 для каждого отдельного значения
для каждого отдельного значения 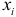 признака
признака 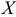 и воспользовавшись отклонениями данных значений
и воспользовавшись отклонениями данных значений 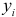 от значений, рассчитанных по уравнению линии регрессии, получим условную дисперсию
от значений, рассчитанных по уравнению линии регрессии, получим условную дисперсию 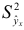 . Она меньше дисперсии
. Она меньше дисперсии 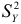 . В качестве показателя интенсивности связи примем нормированное выражение разности этих дисперсий и получим корреляционное отношение, которое применяется для опенки интенсивности нелинейной связи:
. В качестве показателя интенсивности связи примем нормированное выражение разности этих дисперсий и получим корреляционное отношение, которое применяется для опенки интенсивности нелинейной связи:
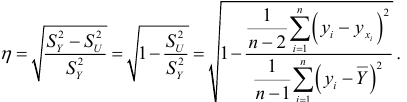
Корреляционное отношение удовлетворяет свойствам:
• Величина корреляционного отношения не зависит от выбора единиц измерения случайных величин 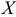 и
и 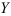 ;
;
• Корреляционное отношение не превосходит единицы, т.е. 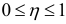 ;
;
• Корреляционное отношение 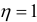 тогда и только тогда, когда между случайными величинами
тогда и только тогда, когда между случайными величинами 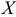 и
и 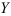 существует функциональная зависимость;
существует функциональная зависимость;
• Если между случайными величинами 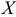 и
и 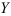 отсутствует хотя бы одна из корреляционных связей, то корреляционное отношение равно нулю;
отсутствует хотя бы одна из корреляционных связей, то корреляционное отношение равно нулю;
• Условие 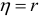 является необходимым и достаточным условием линейной регрессионной связи;
является необходимым и достаточным условием линейной регрессионной связи;
• Корреляционное отношение не меньше коэффициента корреляции 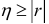
Из свойств корреляционного отношения следует, что чем больше значение корреляционного отношения приближается к единице (т. е. чем ближе нормированная разность 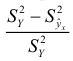 к единице), тем сильнее наблюдаемая связь, а если
к единице), тем сильнее наблюдаемая связь, а если 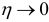 , то связь ослабевает. При функциональной зависимости все значения
, то связь ослабевает. При функциональной зависимости все значения 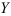 лежали бы на линии регрессии.
лежали бы на линии регрессии.
Для оценки интенсивности нелинейной связи используется также индекс корреляции 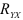 , который вычисляется по формуле:
, который вычисляется по формуле:
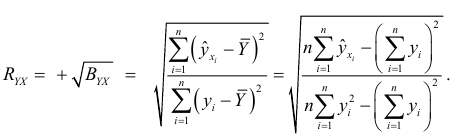
Индекс корреляции принимает значения в интервале
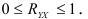
Если 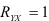 , т.е.
, т.е. 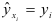 , для всех
, для всех 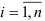 , то мы располагаем функциональной зависимостью. Если же
, то мы располагаем функциональной зависимостью. Если же 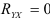 , т.е.
, т.е. 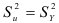 для всех
для всех 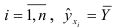 , то связь в этом случае отсутствует. Чем больше значение индекса корреляции приближается к единице, тем сильнее наблюдаемая связь. Средняя квадратичная ошибка корреляционного отношения
, то связь в этом случае отсутствует. Чем больше значение индекса корреляции приближается к единице, тем сильнее наблюдаемая связь. Средняя квадратичная ошибка корреляционного отношения
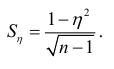
Различные уравнения регрессии, служащие для оценки уровня величин исследуемых зависимых переменных, представляют большей практический интерес, например в планировании. Оценки, полученные в уравнении регрессии, достаточно точно воспроизводят линию реальной эволюции явлений, если не слишком отдаляться от эмпирических данных. Экстраполяция допускается только тогда, когда доказана полная аналогия условий, места, времени и однородности явлений, к которым относятся оценки.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

