Оглавление:
Некоторые приложения векторного произведения
Установление коллинеарности векторов
Если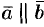 
, то 
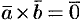(и наоборот), т. е.
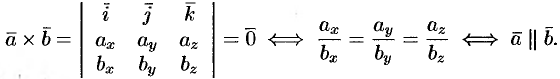
Нахождение площади параллелограмма и треугольника
Согласно определению векторного произведения векторов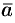 
и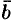 
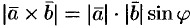, т. е. 
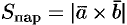. И, значит, 
.
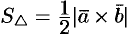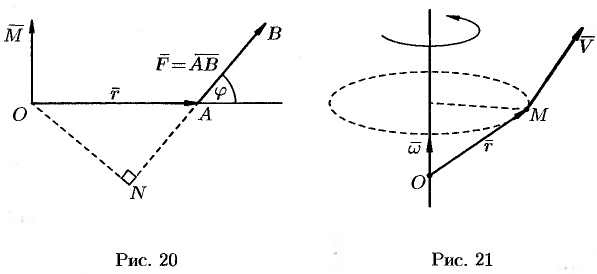
Определение момента силы относительно точки
Пусть в точке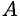 
приложена сила 
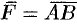и пусть 
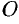— некоторая точка пространства (см. рис. 20).
Из физики известно, что моментом силы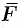 
относительно точки 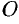называется вектор 
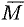, который проходит через точку 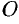и:
1) перпендикулярен плоскости, проходящей через точки , ,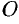 
;
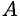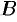2) численно равен произведению силы на плечо
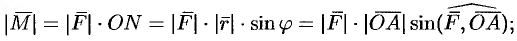
3) образует правую тройку с векторам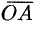и 
и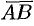 
.
Стало быть,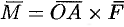 
.
Нахождение линейной скорости вращения
Скорость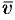 
точки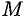 
твердого тела, вращающегося с угловой скоростью 
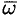вокруг неподвижной оси, определяется формулой Эйлера 
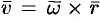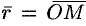, где 
, где 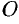— некоторая неподвижная точка оси (см. рис. 21).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Абсолютная и условная сходимости числовых рядов |
| Выражение векторного произведения через координаты |
| Выражение смешанного произведения через координаты |
| Некоторые приложения смешанного произведения |
