Оглавление:
Некоторые приложения тройного интеграла
Объем тела
Объем области  выражается формулой
выражается формулой 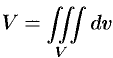 или
или
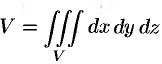 — в декартовых координатах,
— в декартовых координатах,
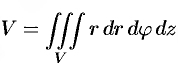 — в цилиндрических координатах,
— в цилиндрических координатах,
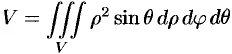 — в сферических координатах.
— в сферических координатах.
Масса тела
Масса тела 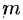 при заданной объемной плотности
при заданной объемной плотности 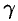 вычисляется с помощью тройного интеграла как
вычисляется с помощью тройного интеграла как
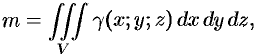
где 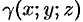 — объемная плотность распределения массы в точке
— объемная плотность распределения массы в точке 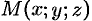 .
.
Статические моменты
Моменты 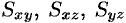 тела относительно координатных плоскостей
тела относительно координатных плоскостей 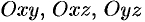 вычисляются по формулам
вычисляются по формулам
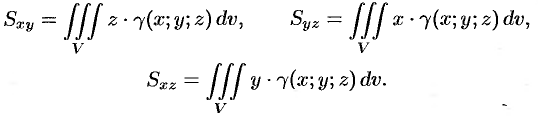
Центр тяжести тела
Координаты центра тяжести тела  находятся по формулам
находятся по формулам
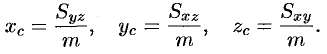
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
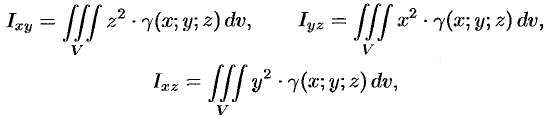
а моменты инерции относительно координатных осей:
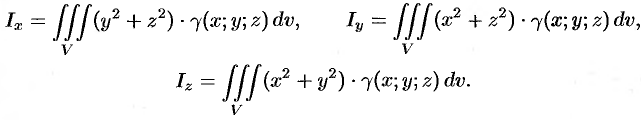
Пример №54.4.
Найти объем тела, ограниченного поверхностями 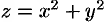 и
и 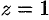 .
.
Решение:
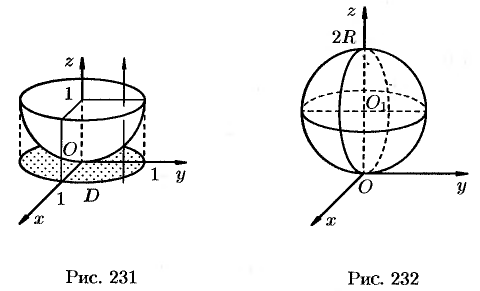
Данное тело ограничено сверху плоскостью 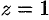 , снизу — параболоидом
, снизу — параболоидом 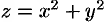 (см. рис. 231). Объем тела находим, используя цилиндрические координаты:
(см. рис. 231). Объем тела находим, используя цилиндрические координаты:
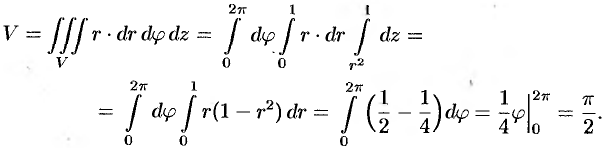
Пример №54.5.
Найти массу шара 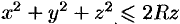 , если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
, если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
Решение:
Уравнение сферы 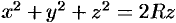 можно записать так:
можно записать так: 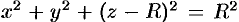 . Центр шара расположен в точке
. Центр шара расположен в точке 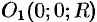 (см. рис. 232). Пусть
(см. рис. 232). Пусть 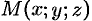 — произвольная точка шара. Тогда, по условию, плотность
— произвольная точка шара. Тогда, по условию, плотность 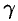 определяется формулой
определяется формулой
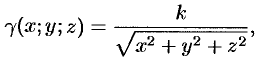
где 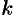 — коэффициент пропорциональности,
— коэффициент пропорциональности, 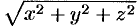 — расстояние от точки
— расстояние от точки  до начала координат.
до начала координат.
Итак, 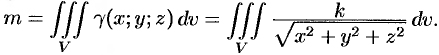
Вычислять интеграл будем в сферических координатах. Уравнение сферы 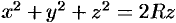 примет вид
примет вид 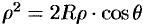 , т. е.
, т. е. 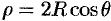 .
.
Поэтому сферические координаты будут изменяться в следующих пределах: 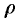 — от 0 до
— от 0 до 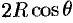 ;
; 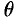 — от 0 до
— от 0 до 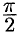 ;
; 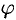 — от 0 до
— от 0 до 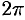 . Подынтегральная функция примет вид
. Подынтегральная функция примет вид 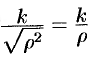 . Поэтому
. Поэтому
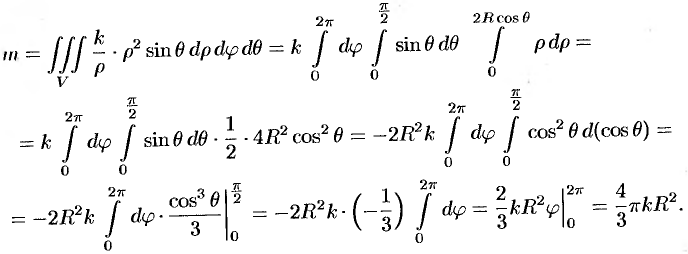
Из соображений симметрии следует, что 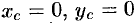 ; вычислив интеграл
; вычислив интеграл 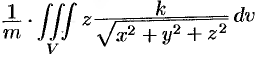 , найдем
, найдем 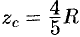 . Итак, координаты центра тяжести
. Итак, координаты центра тяжести 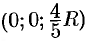 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

