Оглавление:
Некоторые приложения степенных рядов
Приближенное вычисление значений функции
Пусть требуется вычислить значение функции  при
при 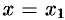 с заданной точностью
с заданной точностью 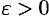 .
.
Если функцию  в интервале
в интервале 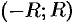 можно разложить в степенной ряд
можно разложить в степенной ряд
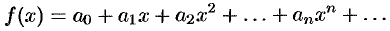
и 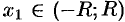 , то точное значение
, то точное значение 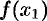 равно сумме этого ряда при
равно сумме этого ряда при 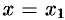 , т. е.
, т. е.
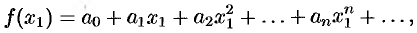
а приближенное — частичной сумме  , т.е.
, т.е.
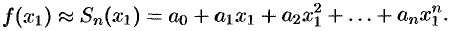
Точность этого равенства увеличивается с ростом  . Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
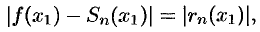
где
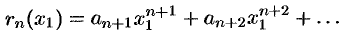
Таким образом, ошибку 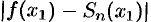 можно найти, оценив остаток
можно найти, оценив остаток 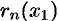 ряда.
ряда.
Для рядов лейбницевского типа
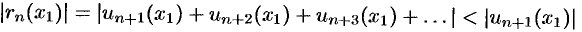
(см. п. 61.1).
В остальных случаях (ряд знакопеременный или знакоположительный) составляют рад из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. И в качестве оценки 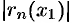 берут величину остатка этого нового ряда.
берут величину остатка этого нового ряда.
Пример №65.1.
Найти 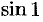 с точностью до 0,001.
с точностью до 0,001.
Решение:
Согласно формуле (64.5),
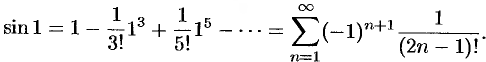
Стоящий справа ряд сходится абсолютно (проверить самостоятельно). Так как 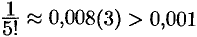 , a
, a 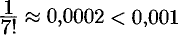 , то для нахождения
, то для нахождения 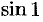 с точностью до 0,001 достаточно первых трех слагаемых:
с точностью до 0,001 достаточно первых трех слагаемых:
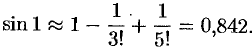
Допускаемая при этом ошибка меньше, чем первый отброшенный член (т.е. меньше, чем 0,0002). Вычисленное микрокалькулятором значение 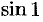 примерно равно 0,84147.
примерно равно 0,84147.
Пример №65.2.
Вычислить число 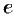 с точностью до 0,001.
с точностью до 0,001.
Решение:
Подставляя 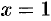 в формулу (64.4), получим:
в формулу (64.4), получим:
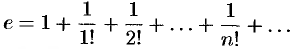
Справа стоит знакоположительный ряд. Возьмем  слагаемых и оценим ошибку
слагаемых и оценим ошибку 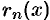 :
:
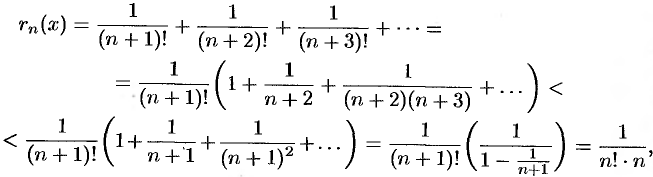
т. е. 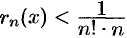 . Остается подобрать наименьшее натуральное число
. Остается подобрать наименьшее натуральное число  , чтобы выполнялось неравенство
, чтобы выполнялось неравенство 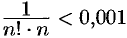 .
.
Нетрудно вычислить, что это неравенство выполняется при 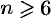 . Поэтому имеем:
. Поэтому имеем:
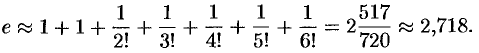
Замечание. Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена
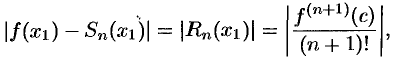
где 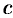 находится между 0 и
находится между 0 и 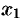 . В последнем примере
. В последнем примере 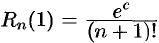 ,
,  . Так как
. Так как 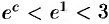 , то
, то 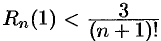 . При
. При 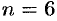 имеем:
имеем:
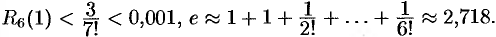
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

